| |

LA DIVISIÓN
|

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
[Registrate
aquí]
Entrar a exámenes
de:
Contenido Revisado 
|
|
|
División por 0, 1, 2 y 3
Dividir es separar un número en
varios grupos iguales.
Cuando dividimos 6 por 3 estamos separando 6 en 3 grupos
iguales de 2.
Hay dos formas comunes de escribir
el signo de la división.
El número 6 dividido 3 se podría escribir como 6/3 o 6 ÷ 3.
dicho en palabras (seis entre tres)
Dividir por 0
No se pueden dividir números por 0
porque es imposible hacer 0 grupos de una cantidad.
Dividir por 1
Cualquier número dividido por 1 es
igual a ese número. Si divides por 1 tienes un grupo y por
lo tanto todo está en ese grupo.
Dividir por 2 y 3
Los datos para las divisiones por
dos y tres se encuentran en la siguiente tabla.
|
DOS |
| 0 ÷ 2 = 0 |
2 ÷ 2 = 1 |
4 ÷ 2 = 2 |
6 ÷ 2 = 3 |
8 ÷ 2 = 4 |
| 10 ÷ 2 = 5 |
12 ÷ 2 = 6 |
14 ÷ 2 = 7 |
16 ÷ 2 = 8 |
18 ÷ 2 = 9 |
|
TRES |
| 0 ÷ 3 = 0 |
3 ÷ 3 = 1 |
6 ÷ 3 = 2 |
9 ÷ 3 = 3 |
12 ÷ 3 = 4 |
| 15 ÷ 3 = 5 |
18 ÷ 3 = 6 |
21 ÷ 3 = 7 |
24 ÷ 3 = 8 |
27 ÷ 3 = 9 |
Dividir por 4, 5 y 6
Los datos para las divisiones por
cuatro, cinco y seis se encuentran en la siguiente tabla.
|
CUATRO |
| 0 ÷ 4 = 0 |
4 ÷ 4 = 1 |
8 ÷ 4 = 2 |
12 ÷ 4 = 3 |
16 ÷ 4 = 4 |
| 20 ÷ 4 = 5 |
24 ÷ 4 = 6 |
28 ÷ 4 = 7 |
32 ÷ 4 = 8 |
36 ÷ 4 = 9 |
|
CINCO |
| 0 ÷ 5 = 0 |
5 ÷ 5 = 1 |
10 ÷ 5 = 2 |
15 ÷ 5 = 3 |
20 ÷ 5 = 4 |
| 25 ÷ 5 = 5 |
30 ÷ 5 = 6 |
35 ÷ 5 = 7 |
40 ÷ 5 = 8 |
45 ÷ 5 = 9 |
|
SEIS |
| 0 ÷ 6 = 0 |
6 ÷ 6 = 1 |
12 ÷ 6 = 2 |
18 ÷ 6 = 3 |
24 ÷ 6 = 4 |
| 30 ÷ 6 = 5 |
36 ÷ 6 = 6 |
42 ÷ 6 = 7 |
48 ÷ 6 = 8 |
54 ÷ 6 = 9 |
Dividir por 7, 8 y 9
Los datos para las divisiones por
siete, ocho y nueve se encuentran en la siguiente tabla..
|
SIETE |
| 0 ÷ 7 = 0 |
7 ÷ 7 = 1 |
14 ÷ 7 = 2 |
21 ÷ 7 = 3 |
28 ÷ 7 = 4 |
| 35 ÷ 7 = 5 |
42 ÷ 7 = 6 |
49 ÷ 7 = 7 |
56 ÷ 7 = 8 |
63 ÷ 7 = 9 |
|
OCHO |
| 0 ÷ 8 = 0 |
8 ÷ 8 = 1 |
16 ÷ 8 = 2 |
24 ÷ 8 = 3 |
32 ÷ 8 = 4 |
| 40 ÷ 8 = 5 |
48 ÷ 8 = 6 |
56 ÷ 8 = 7 |
64 ÷ 8 = 8 |
72 ÷ 8 = 9 |
|
NUEVE |
| 0 ÷ 9 = 0 |
9 ÷ 9 = 1 |
18 ÷ 9 = 2 |
27 ÷ 9 = 3 |
36 ÷ 9 = 4 |
| 45 ÷ 9 = 5 |
54 ÷ 9 = 6 |
63 ÷ 9 = 7 |
72 ÷ 9 = 8 |
81 ÷ 9 = 9 |
Dividir decenas
¿Como dividir un número
formado por decenas exáctas por otro número?
- Mover el punto decimal del
dividendo un lugar hacia la izquierda.
- Lleva a cabo la división.
- Mueve el punto decimal del
cociente un lugar hacia la derecha.
División
¿Como dividir un número de dos
dígitos por un número de un dígito? (ej. 42 ÷7).
- Coloca el divisor (7) antes del
signo divisor y coloca el dividendo (42) debajo del
mismo.
- Examina el primer dígito del
dividendo (4). Si es más pequeño que 7 no se puede
dividir por siete y obtener un número natural.
Multiplica el 6 por 7 y coloca el
resultado (42) debajo del 42 del dividendo.
Traza una línea debajo del 42 y
réstaselo al 42 (42-42=0). Como el resultado es 0 la
división se termina y 6 es la respuesta.
Dividir centenas
Como dividir un número formado por
centenas exáctas por otro número.
- Mueve el punto decimal del
dividendo dos lugares hacia la derecha.
- Lleva a cabo la división.
- Mueve el punto decimal del
cociente dos lugares hacia la derecha.
División
Como dividir un número de tres
dígitos por un número de un dígito (e.g. 416 ÷ 7).
- Coloca el divisor (7) antes del
signo divisor y coloca el dividendo (416) debajo del
mismo.
- Examina el primer dígito del
dividendo (4). Es más pequeño que 7 tan no pueden ser
divididos entre 7 en producir un número entero. Tome
luego los primeros dos dígitos del dividendo (41) y
encuentre cuántos 7's es contiene. En este caso 41
asideros cinco sietes (5*7=35) pero no seis (6*7=42).
Coloque el 5 encima del paréntesis de la división.
- Multiplique el 5 por 7 y
coloque el resultado (35) debajo del 41 del dividendo.
- Escriba un línea bajo el 35 y
lo resta de 41 (41-35=6). Baje el 6 del 416 y lo coloca
a la derecha del otro 6.
- Divida 66 por 7 y coloque esa
respuesta encima del paréntesis de la división a la
derecha del cinco.
- Multiplique el 9 del cociente
por el divisor (7) en obtener 63 y colocar esto debajo
del 66. Reste 63 de 66 en dar una respuesta de 3. El
número 3 son llamados el resto e indican eso había tres
izquierdo sobre.
División
Cómo dividir un número de tres
dígitos por un número de un dígito (e.g 413 ÷ 7).
- Coloca el divisor delante del
signo divisor y coloca el dividendo (413) debajo del
mismo.
- Examina el primer dígito del
dividendo (4). Es menor que 7 entonces no se puede
dividir por 7 y obtener un número entero. Luego toma los
primeros dos dígitos del dividendo (41) y determina
cuantos sietes contiene. En este caso 41 contiene cinco
sietes (5 X 7= 35) pero no seis (6 X 7= 42).
- Multiplica el 5 por el 7 y
coloca el resultado (35) debajo del 41 del dividendo.
- Traza una línea debajo del 35 y
réstalo del 41 (41-35=6). Baja el 3 del 413 y colócalo a
la derecha del 6.
- Divide 63 por 7 y coloca la
respuesta sobre el signo divisor a la derecha del cinco.
- Multiplica el 9 del cociente
por el divisor (7) para obtener 63 y colócalo debajo del
63 debajo del dividendo. Resta 63 del 63 y obtiene un
resultado de 0. Esto indica que no queda nada y que el
siete se puede dividir exactamente por 413 para producir
un cociente de 59.
Un niño notable
La
división: una operación para repartír
Carlos Federico Gauss fue un matemático alemán al que se le llamó "el
príncipe de los matemáticos".
 Un
día, cuando tenía 10 años, su profesor le dio un ejercicio en clases
para tener ocupado a sus alumnos durante largo tiempo: calcular la suma
de la serie de los números naturales del 1 al 100. Un
día, cuando tenía 10 años, su profesor le dio un ejercicio en clases
para tener ocupado a sus alumnos durante largo tiempo: calcular la suma
de la serie de los números naturales del 1 al 100.
Gauss terminó su trabajo a los pocos minutos. El profesor no se podía
convencer.
¿Qué había hecho este pequeño genio?
Muy simple: sumó los números extremos de la serie. Así:
1 +
100 = 101
2 +
99 =
101
3 +
98 =
101...
Y el resultado era siempre
101.
Si el resultado se repetía
50 veces pensó: la
suma corresponde a 101
x 50.
Y eso da un total de 5,050
El profesor quedó maravillado con su precoz alumno.
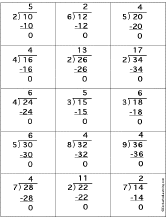
Muestras
|
1:
|
|
024
9 )216
0
21
18
36
36
0
|
|
|
2:
|
|
038
9 )342
0
34
27
72
72
0
|
|
|
3:
|
|
017
6 )102
0
10
6
42
42
0
|
|
|
4:
|
|
029
9 )261
0
26
18
81
81
0
|
|
|
|
|
|
7:
|
|
045
8 )360
0
36
32
40
40
0
|
|
|
8:
|
|
027
6 )162
0
16
12
42
42
0
|
|
|
Los secretos de la división
La división tiene como elementos:
dividendo : divisor = cuociente
Cuando el divisor no cabe exactamente en el dividendo, queda un resto
o residuo debajo de él.
Dos casos
En la división de decimales podemos encontrar dos casos:
-
Que dividendo y divisor sean enteros y en el cuociente obtengamos
decimales.
-
Que dividendo o divisor sea decimal, o ambos cumplan esa condición.
Analizaremos ambos.
Dividendo y divisor enteros, con cuociente decimal
Encontraremos este caso en divisiones inexactas de enteros, en las que
para obtener un cuociente más específico, es necesario seguir
dividiendo.
Por ejemplo:
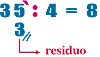
Es división inexacta; quedó de residuo el 3.
¿Cómo seguir dividiendo si no hay más cifras en el
divisor?
Si las hay. Recuerda que los enteros son decimales periódicos, de
la siguiente forma:
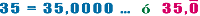
|
|
|
Para
continuar dividiendo, bajamos el primer 0 decimal al lado del 3,
colocamos la coma en el cuociente y seguimos dividiendo. Así:
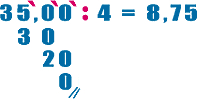
|
En
este ejemplo tuvimos que sacar dos cifras decimales y logramos un
decimal exacto. Es más específico el cuociente 8,75 que 8.
Cuando llegamos a los milésimos y todavía no tenemos un decimal exacto,
por acuerdo, no continuamos la división. Si quieres obtener un resultado
con más cifras decimales, aprovecha de usar la calculadora.
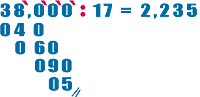
|
|
Algunas
veces se nos presenta un dividendo menor al divisor. Entonces,
inmediatamente colocamos 0 en el cuociente, la coma y escribimos la
parte decimal del dividendo para continuar.
Veamos qué sucede con :

Cuando hayas aprendido la forma de solución, no será necesario escribir
la parte decimal con ceros; lo harás mentalmente. |
Sin calculadora
Tú ya sabes que la división es la operación inversa de la
multiplicación. Entonces, recurriremos a ella para comprobar resultados.
Sólo debes multiplicar el cuociente por el divisor, luego le adicionas
el residuo -si hay- y la suma deberá coincidir con el dividendo.
Revisemos el ejemplo anterior de 38 : 17. Su cuociente era
2,235 y el residuo, 5.
Entonces, multiplicamos:

¡Bien! |
|
|