Parábola
Fecha de primera versión: 02-04-98
Fecha de última actualización: 19/04/2010
![]()
La elipse, la parábola y la hipérbola se llaman secciones cónicas. La razón de este nombre es que estas curvas se forman al seccionar un cono por un plano.
Otra forma de definir estas curvas (en vez de como secciones de un cono) es como la curva que describe un punto que se mueve en un plano de manera que el cociente entre las distancias de ese punto a un punto fijo (foco) y a una recta (directriz) es constante (excentricidad).
Si esta constante está comprendida entre cero y uno, la curva es una elipse. Si es igual a uno, es una parábola y si es mayor que uno es una hipérbola.
Menaechmo, un discípulo de Platon y Eudoxo, estudió la parábola para resolver el problema de la duplicación del cubo (se trataba de construir un cubo de volumen doble de otro conocido, utilizando los artilugios de la época, o sea, regla y compás).
Euclides también estudió esta curva, pero ha pasado a la historia de la mano de Apolonio de Perga, al que debe su nombre.
Esta es la razón del nombre:
La parábola se puede expresar por esta ecuación y2 = kx, siendo k = 2b2/a. Esto quiere decir que en cualquier punto de la parábola podemos construir un cuadrado de lado y (la ordenada del punto) y un rectángulo de lados x (la abscisa del punto) y k, y las áreas del cuadrado y el rectángulo siempre serán iguales.
Si hacemos lo mismo en una hipérbola el cuadrado siempre será mayor y en una parábola el cuadrado siempre es menor.
Resulta que una de las acepciones de parábola en griego era equiparable, de elipse deficiencia y de hipérbola exceso. De ahí los nombres.
Otros muchos matemáticos la estudiaron: Pappus (el foco y la directriz), Pascal (que la consideró como la proyección de una circunferencia), Galileo (descubrió que los proyectiles describen esta curva), Newton (descubrió que los rayos de luz que se reflejan en una parábola coinciden en el foco).
La ecuación genérica de la parábola, cuyo eje es paralelo al eje y, en coordenadas cartesianas es:
y = ax2 + bx + c
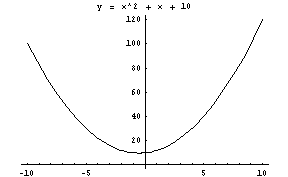
La ecuación genérica de la parábola, cuyo eje es paralelo al eje x, en coordenadas cartesianas es:
(y - y0)2 = 4a(x - x0)
Siendo ( x0, y0) el vértice de la parábola y a la distancia del vértice al foco de la parábola.
La ecuación de la directriz de una parábola es x = - p/2 (si la parábola es del tipo y2 = 2px) o y = -p/2 (si la parábola es del tipo x2 = 2py).
El área de un segmento de parábola es 4/3 el área de un triángulo con la misma base y el mismo vértice.
El área de un segmento de parábola es 2/3 el área del paralelogramo circunscrito.
Propiedades de la parábola
El ángulo formado por la tangente en un punto con la recta paralela al eje de la parábola en ese punto es igual al formado por la tangente con la recta que une el punto de tangencia con el foco de la parábola.
Construcción de una parábola
1- Dibuja un punto y una recta en una hoja de papel.
2- Dobla la hoja de manera que cualquier de la recta coincida con el punto
dibujado.
3- Deshaz la doblez.
4- Repite las operaciones 2 y 3 haciendo coincidir otro punto de la recta con
el punto.
Las marcas que han dejado las dobleces delimitan una parábola. El punto dibujado es el foco de la parábola y la recta es la directriz.
En la página http://www-groups.dcs.st-and.ac.uk/~history/Curves/Curves.html encontrarás todo sobre las curvas.