Investigaciones geométricas de la teoría de paralelas
Fecha de primera versión: 17-06-2004
Fecha de última actualización: 19/04/2010

Investigaciones geométricas de la teoría de paralelas
Autor: Lobachevsky
Publicado en Berlín, en 1840. Editorial Fincke.
Consta de 37 proposiciones.
Comienza con 15 proposiciones, sin demostración.
La proposición 16 define el ángulo de paralelismo: Todas las rectas
trazadas por un mismo punto en un plano pueden distribuirse, con respecto a una
recta dada en dicho plano, en dos clases: rectas que cortan a la recta dada y
rectas que no la cortan. La recta que está en el límite de estas dos clases se
dice paralela a la recta dada.
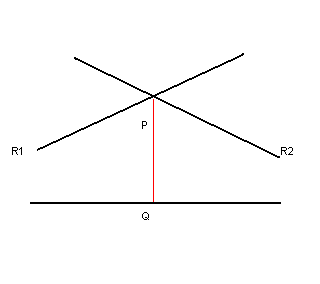 El ángulo de
paralelismo en el punto P con respecto a la recta horizontal es cada uno de los
ángulos agudos que forman, por ambos lados, las rectas paralelas a la
horizontal con la recta PQ.
El ángulo de
paralelismo en el punto P con respecto a la recta horizontal es cada uno de los
ángulos agudos que forman, por ambos lados, las rectas paralelas a la
horizontal con la recta PQ.
En la geometría clásica, el angulo siemprp es recto y en la de Lobachevsky,
siempre es agudo.
En la proposición 17 demuestra que toda linea recta conserva el caracter de
paralelismo en todos sus puntos.
En la proposición 18 demuestra que dos líneaa rectas son simpre
recírpocamente paralelas.
Las proposiciones 19 y 20 se refieren a la suma de los ángulos internos de
un triángulo.
Las proposiciones 21 a 24 tratan de las propiedades del ángulo de
paralelismo.
Las proposiciones 25 a 28 tratan de la geometría del espacio.
Las proposiciones 29 a 31 tratan de la curva límite (horociclo). Curva, en
un plano, tal que todas las perpendiculares elevadas sobre los puntos medios de
las cuerdas, son paralelas entre si. A una cualquiera de esas paralelas se le
llama eje de la curva-límite.
En la proposición 34 define la superficie límite (horesfera). Esfera
engendrada por la revolución de la curva límite alrededor de uno de sus
ejes.
En la proposición 35 obtiene una serie de relaciones trigonométricas.
En la proposición 36 obtiene el ángulo de paralelismo
En la proposición 37 presenta una seríe de relaciones trigonométricas.
Finaliza esta proposición diciendo que la geometría clásica es un caso
particular de la geometría imaginaria.
![]()
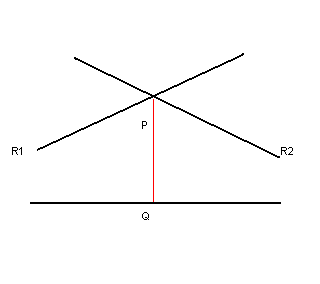 El ángulo de
paralelismo en el punto P con respecto a la recta horizontal es cada uno de los
ángulos agudos que forman, por ambos lados, las rectas paralelas a la
horizontal con la recta PQ.
El ángulo de
paralelismo en el punto P con respecto a la recta horizontal es cada uno de los
ángulos agudos que forman, por ambos lados, las rectas paralelas a la
horizontal con la recta PQ.