MATEMÁTICAS INTEGRADAS 2

Triángulos y Rectángulos

Módulo 1

¿Qué es un triángulo?

El triángulo es un polígono que tiene tres lados y tres ángulos. Es, por tanto, el polígono  más simple y el conocimiento de sus características y propiedades nos ayudará a analizar el triángulo rectángulo.

Propiedades

Recordemos algunas propiedades elementales de los triángulos

v  Los tres ángulos de un triángulo suman 180º .

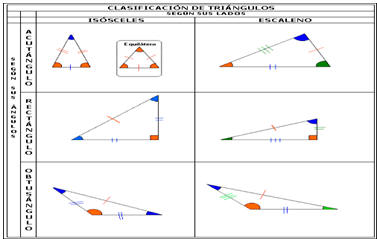
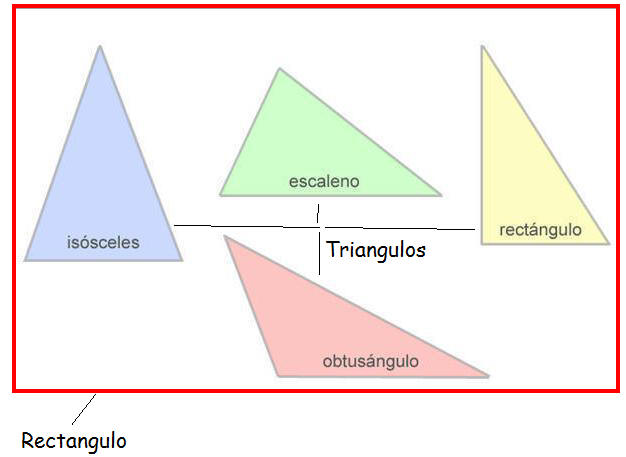
v  El triángulo, como polígono que tiene tres lados y tres ángulos, se clasifica según sus lados y según sus ángulos.

Según sus lados:

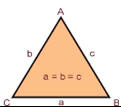
v  Equilátero: Tres lados iguales.

v  Isósceles: Dos lados iguales y el tercero con otra medida.

v  Escaleno: Tres lados con distinta medida.

Según sus ángulos:

v  Rectángulo: Un ángulo recto.

v  Acutángulo: Tres ángulos agudos

v  Obtusángulo: Un ángulo obtuso

Teorema de Pitágoras

Todo el mundo conoce a Pitágoras aunque sólo sea por el teorema que lleva su nombre.

“El área cuadrado construido sobre la hipotenusa de un triángulo rectángulo es igual a la suma de las áreas de los cuadrados construidos sobre los dos catetos".

Antes de profundizar en este teorema por qué no investigamos algo acerca de Pitágoras y de su época.

¿Quién era?, ¿dónde y cuándo vivió?, ¿qué culturas le influyeron?, ¿qué era la escuela pitagórica?, ¿cómo estaban organizados?, ¿qué Matemáticas utilizaron?, ¿qué otros descubrimientos hicieron?, ¿cuáles han llegado hasta nosotros?, ¿cómo y para qué los utilizamos?....

¿Quién fue Pitágoras?

Pitágoras de Samos, 582 a.C - 496 a.C). Fue filósofo y matemático griego que descubrió como hallar la longitud de la hipotenusa.

En un triángulo rectángulo. Nació en la isla de Samos en el año 500 a. C. y hacia el año 530 a. C.  Pitágoras puede ser considerado la persona más influyente de la historia universal, pasa por ser el introductor de pesos y medidas, descubridor de la teoría musical, inventor de la geometría y la aritmética teórica.

Demostración del Teorema de Pitágoras

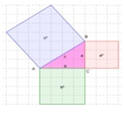
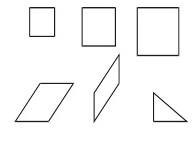
Ahora vamos a realizar una demostración del teorema de Pitágoras haciendo uso de un rompecabezas de seis piezas. Así las piezas que vamos a usar son, el triángulo rectángulo, los cuadrados de lado a, b y h, un paralelogramo de lados el cateto menor a y la hipotenusa h, y por último otro paralelogramo de lados el cateto mayor b y la hipotenusa.

Paso 1- Imprimir el documento adjunto titulado  Demostración 1 Rompecabezas en pdf. También puedes dibujarlas, y/o copiar y pegar en MS Paint. 

Las piezas son:

Es fácilmente comprobable que el área de los paralelogramos es a2 para el menor y b2 para el mayor.

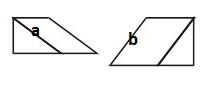
Paso 2- Recorta tus figuras  (las  dos figuras siguientes) y compara la altura del paralelogramo a  con la altura del paralelogramo b.  ¿Cuál es mayor?

Si contestaste  b estas correcto.

Se ve claramente como la altura del paralelogramo menor es a, y que la altura del paralelogramo mayor es b, así pues como el área de un paralelogramo es base por altura, tenemos que estos paralelogramos tienen áreas a2 y b2 respectivamente.

Ahora vamos a ver con la siguiente figura como el área del cuadrado de lado h coincide con la suma de las áreas de los paralelogramos.

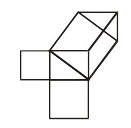
Como podemos observar es esta figura la colocación estratégica de los dos paralelogramos, hacen visible que la suma de sus áreas coincide con el área del cuadrado de lado h. Así pues tenemos el resultado del Teorema de Pitágoras, es decir, h2=a2+b2.

Teorema de Pitágoras es el siguiente: En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Ejemplo: Hallar  la hipotenusa  

Encontrar el valor de la hipotenusa de un triángulo rectángulo en donde el valor del cateto a es igual a 5 unidades y el valor del cateto b son igual a 9 unidades

a= 5 unidades

b= 9 unidades

c=  X

La suma del cuadrado de los dos catetos es igual a la hipotenusa al cuadrado

a² + b² = c²    

Hallar el cateto

Encontrar el valor del cateto a de un triángulo rectángulo en donde el valor del cateto b es igual a 5 unidades y el valor de la hipotenusa es igual a 7

a= x unidades

b= 5 unidades

c= 7 unidades

a² + b² = c²

A partir de este resultado, la demostración del teorema de Pitágoras no es más que un simple cálculo.

AB2+AC2=BC.(BH+CH)=BC.BC=BC2.

Ejemplo 1:

Calculamos la longitud de una escalera, sabiendo que está apoyada en la pared a una distancia de 1.8 m y alcanza una altura de 7 m

Aplicamos el teorema de Pitágoras:

h2 = (1,8)2 + 72 = 52.24

h = 52, 24 = 7 .23 m

La escalera mide 7.23 m.

Ejemplo 2:

Una antena está sujeta al suelo por dos cables que forman un ángulo recto de longitudes 27 y 36 cm. ¿Cuál es la distancia que separa los dos puntos de unión de los cables con el suelo?

Si giramos el triángulo, obtenemos un triángulo rectángulo en el que la hipotenusa es la distancia entre los dos cables.

27 2 + 36 2 = a 2 → a 2 = 2.025 → a = 2.025 → a = 45 cm

Ejemplo 3

Calcula  la altura de un triángulo equilátero de lado 10 cm. En el triángulo equilátero ABC  lado 10 cm, vemos que la altura AH es un eje de simetría y, por tanto, el punto medio del lado BC es H, siendo la longitud HC igual a 5 cm.

Aplicando el teorema de Pitágoras en el triángulo AHC, que es rectángulo:

A H = 10 2 - 5 2 = 100 - 25 = 75 = 8. 66 cm

La altura AH del triángulo equilátero mide 8.66 cm.

Triple Pitagóricos

Un triple pitagórico es un triple de números naturales a, b, c que satisface a² + b² = c². El triple es primitivo si a, b, c no tienen factor común > 1. El conjunto de tres números positivos que satisfacen la fórmula de Pitágoras se conoce como un triple pitagórico. El código siguiente creado en el lenguaje de Delphi encuentra los primeros 20 triples pitagóricos.

Plano de Coordenadas

Para especificar un punto en un plano nos valdremos de un plano de las  coordenadas rectangulares formado al intersecar perpendicularmente por el origen de ambas a dos rectas numéricas en el plano. A una de las rectas la representamos horizontalmente y la llamamos el eje de abscisas o eje de x. A la otra recta la representamos verticalmente y la llamamos el eje de ordenadas o eje de y.

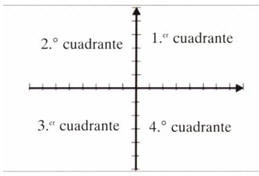
La utilidad del plano de las  coordenadas rectangulares, puede ilustrarse de la siguiente manera: Dos personas acuerdan encontrarse a las 4:00pm, en cierta esquina de una ciudad cuyo sistema vial está constituido por calles paralelas y avenidas perpendiculares a las calles, como en el dibujo.

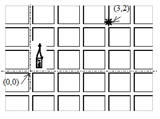
Entonces, la ubicación del sitio de encuentro es en la avenida 4 con calle 3.

Si las calles y avenidas no estuvieran numeradas, sino que se identificaran por nombres, aunque las personas del encuentro no recordaran, sería posible identificar con precisión el punto de encuentro, si se toma como punto de referencia la catedral, un hospital y una escuela, por ejemplo: La ubicación sería: dos cuadras arriba de la iglesia y tres cuadras a la derecha. Asignando el punto (0,0) a la esquina de la iglesia; en ese caso, el punto de encuentro tendría coordenadas (3,2), lo que sería equivalente a decir; tres cuadras  a la derecha y dos cuadras hacia arriba.

Fórmula de  Distancia

Ejemplo:

Aplicar la fórmula de la distancia en el plano cartesiano para hallar la distancia entre los puntos.

Encuentra la distancia entre los puntos (1, 1) y (5 ,4)

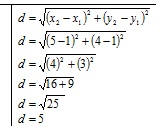
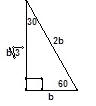
Triángulo 30⁰-60⁰-90⁰

En un triángulo de 30⁰-60⁰-90⁰ la medida de la hipotenusa es de dos veces la medida del lado más corto.  Las medida del lado más largo es √3 veces la medida del lado más corto.

Triángulo 45⁰-45⁰-90⁰

En un triángulo de 45⁰-45⁰-90⁰ la medida de la hipotenusa es √2 veces la medida de los lados.

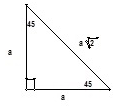
Ejemplo 1:

Encuentre la longitud de la hipotenusa de un triángulo rectángulo si las longitudes de los otros dos lados son de 4 pulgadas.

También puede reconocer un 30 ° - 60 ° - 90 ° por los ángulos del triángulo.  Un triángulo rectángulo con un  ángulo de 30 o 60  o 90 grados es un triángulo rectángulo especial.

 Razones Trigonométricas

Imagina  que elevas una cometa. Hay un viento fuerte, por lo tanto la cuerda está

tensa. Has marcado la cuerda,  sabes cuánta cuerda has soltado y puedes medir el ángulo que forma la cuerda con la horizontal.

Entonces  puedes usar una razón trigonométrica para hallar la altura de la cometa. La trigonometría relaciona las medidas angulares de los triángulos rectángulos con las longitudes de sus lados.

Trigonometría: Esta palabra se la debemos al matemático alemán Pitiscus 1600 D.C. y significa Medida de triángulos.

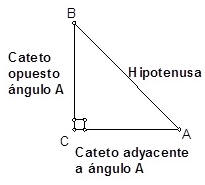
Todo los Triángulos Rectángulos son semejantes, Pero su tamaño no depende de la medida de sus lados sino de la medida de sus ángulos.

Dos triángulos son semejantes si sus ángulos son iguales uno a uno, respectivamente; los lados opuestos a dichos ángulos son proporcionales. Una razón trigonométrica es una razón de las longitudes de dos lados de un triángulo rectángulo.

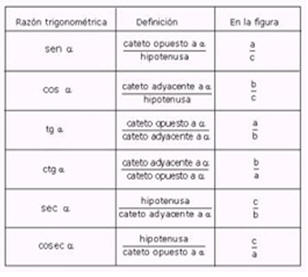
Las tres razones trigonométricas básicas son el seno, el coseno, y la tangente. Éstas se abrevian como sen, cos y tan

Las tres funciones más importantes en trigonometría son el seno, el coseno y la tangente.

Cada una es la longitud de un lado dividida entre la longitud de otro... ¡sólo tienes que aprenderte qué lados son!

Nota: el seno se suele denotar sin (θ)  (por la palabra inglesa "sine").

Pensaras que te será difícil recordar las fórmulas para un examen, pero  si te aprendes la palabra Sohcahtoa ...¿qué?    ¡Sólo es una manera de recordar qué lados se dividen! Así:

Apréndete "" - ¡te puede ayudar en un examen!

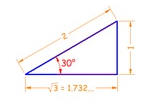
Ejemplo 1: ¿cuáles son el seno, coseno y tangente de 30° ? El triángulo clásico de 30° tiene hipotenusa de longitud 2, lado opuesto de longitud 1 y lado adyacente de longitud √3:

(¡Saca la calculadora y compruébalo!)

Ejemplo 2: cuáles son el seno, coseno y tangente de 45°

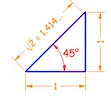
El triángulo  de 45° tiene dos lados de 1 e hipotenusa √2:

Ejemplo: ¿cuáles son el seno, coseno?

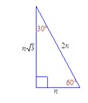
Puedes usar el triángulo de la derecha para hallar el seno y el coseno de 42°. Primero, usa el teorema de Pitágoras para hallar la longitud, h, de la hipotenusa.

Para el ángulo de 42°, el cateto opuesto tiene una longitud de 9 y el cateto

adyacente tiene una longitud de 10.

Solución de Problemas Verbales

La trigonometría de los triángulos rectángulos se utiliza frecuentemente para encontrar la altura de un objeto alto de manera indirecta. Para resolver un problema de este tipo, mide el ángulo desde la horizontal hasta tu recta de visión, cuando veas la parte superior o inferior del objeto. Si miras hacia arriba, medirás el ángulo de elevación. Si miras hacia abajo, medirás el ángulo de depresión.

Lee el ejemplo atentamente. Intenta resolver el problema por tu cuenta, antes de leer la solución.

Ejemplo:

El sonar de un barco de salvamento localiza los restos de un naufragio en un ángulo de depresión de 12°. Un buzo es bajado 40 metros hasta el fondo del mar. ¿Cuánto necesita avanzar el buzo por el fondo para encontrar los restos del naufragio?

Solución

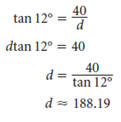
El buzo necesita avanzar aproximadamente 188 metros para llegar a los restos del naufragio.

Aplicación;

Asignación: Valor 15 pts.

Completa la tabla de acuerdo a lo que se te pide.

Contestación

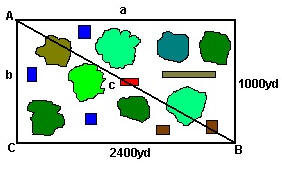
1-Combate de incendios

Para combatir un incendio forestal, el Departamento de Silvicultura desea talar un terreno rectangular alrededor del incendio, como vemos en la  figura. Las cuadrillas cuentan con  equipos de  radiocomunicación de 3000 yardas de alcance. ¿Pueden seguir en contacto las cuadrillas en los puntos A y B?

Contestación:

a2+b2=c2

24002+10002=c2

6, 760,000=c2

c=2600

Las dos cuadrillas están a 2600 yardas de distancia. Esa distancia es menor que la del alcance de los radios, por lo que las cuadrillas se pueden comunicar.

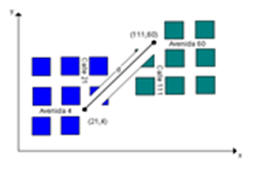
2- Construcción de una vía rápida

En una ciudad, las calles van de norte a sur y las avenidas de este a oeste. Las calles y avenidas tienen 750 pies de separación entre sí. El gobierno de la ciudad desea construir una vía rápida desde el cruce de la Calle 21 con la avenida 4, hasta el cruce de la Calle 111 con la avenida 60. ¿Qué longitud tendrá la vía rápida?

Contestación

d2=(x2-x1)2+ (y2-y1)2 

d2= (111-21)2+ (60-4)2

d2=8100+3136

d=106

 instrucciones: Hallar la distancia  entre los puntos  

Contestación

Dibuja un triángulo rectángulo isósceles. Luego, usa el triángulo para hallar el seno, el coseno y la tangente de 45°.

Solución

Todos los triángulos rectángulos isósceles son semejantes, de

 manera que puedes dibujar uno de cualquier tamaño. Por ejemplo,

usa catetos de longitud 1. Luego, halla la longitud de la hipotenusa.

Solución

El cateto opuesto y el cateto adyacente tienen ambos una longitud de 1.

Resuelve cada triángulo rectángulo.  Haz un dibujo de la figura antes de resolverlo.

En cada caso, C = 90o.

1- A = 28o, c = 17.4 pies

3- B = 82o 51’, c = 4.825 cm

4- La escalera de un coche de bomberos está apoyada contra una pared. Halla la distancia que sube la escalera sobre la pared si forma un ángulo de 43o50’ con respecto al piso.

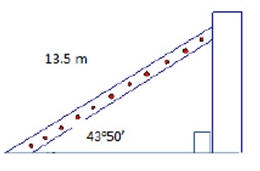
Solución:

1- B = 62o

a = 17.4 sen (28o ),

b = 17.4 cos(28o )

2- A= 44o

a =29.7 cos (46)

b = 29.7 sen (46)

3- A= 7.15o

a = 4.825 cos (82.85 o)

b = 4.825 sen (82.85 o)

4- 13.5 sen (43.83) = 9.35 metros

© Derechos Reservados

Escuela Virtual de Educación Acelerada Proyecto Salón Hogar Inc.