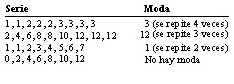MATEMÁTICAS INTEGRADAS 2

EXPERIMENTOS Y ESTUDIO DE OBSERVACIÓN

Módulo 2

Escalas de Medición

Las  características  personales   como estatura , edad, genero, habilidades,  tamaños   de  un  determinado  grupo se  les  puede identificar como variables,   la aplicación  de   medir   característica   y valores    permiten  medir  de  mejor  manera  un   resultado  obtenido. Los niveles de medición son las escalas nominal, ordinal, de intervalo y de razón.

Escala se define como cualquier recurso para determinar la magnitud o cantidad de un objeto o hecho de cualquier clase; instrumento para asignar un número  que indicará cuánto hay de algo; un recurso de medición que provee un conjunto de normas (numeradas de acuerdo con ciertas reglas de trabajo) con las que se puede comparar el objeto que será medido, para asignarle un número o valor matemático que represente su magnitud.

En la estadística descriptiva y con el fin de realizar pruebas de significancia, las variables se clasifican de la siguiente manera de acuerdo con su nivel de medida:

Ø  Escala nominal

Ø  Escala  ordinal

Ø  Escala  intervalo

Ø  Escala de razón

Escala Nominal

El nivel nominal de medición, de la palabra latina común (nombre) describe variables de naturaleza categórica que difieren en calidad más que en cantidad (Salkind, 1998: 113)  En este nivel de medición se establecen categorías distintivas que no implican un orden específico. En el  nivel nominal, las observaciones únicamente se pueden clasificar o contar.

Escala Ordinal

El nivel ordinal describe las variables  sobre el que se pueden ordenar los valores. Se establecen categorías con dos o más niveles que implican un orden inherente entre sí.

La escala de medición ordinal es cuantitativa, porque permite ordenar a los eventos en función de la mayor o menor posesión de un atributo o característica.

Ejemplo 1:

Los autos deben pintarse de color negro,  puede marcar su respuesta de acuerdo a las siguientes alternativas:

___ Totalmente de acuerdo
___ De acuerdo
___ Indiferente
___ En desacuerdo
___ Totalmente en desacuerdo

Las anteriores alternativas de respuesta pueden codificarse con números que van del uno al cinco que sugieren un orden preestablecido pero no implican una distancia entre un número y otro.

Escala Intervalo

El nivel de intervalo procede del latín intervalo lun (espacio entre dos paredes). Este nivel integra las variables que pueden establecer intervalos iguales entre sus valores. Posee las características de la medición nominal y ordinal. Establece la distancia entre una medida y otra. La escala de intervalo se aplica a variables continuas pero carece de un punto cero absoluto.

Escala de Razón

El nivel de razón, cuya denominación procede del latín ratio (cálculo), integra aquellas variables con intervalos iguales pueden situar un cero absoluto. Incluye las características de los tres anteriores niveles de medición anteriores (nominal, ordinal e intervalo). Determina la distancia exacta entre los intervalos de una categoría. Adicionalmente tiene un punto cero absoluto, es decir, en el punto cero no existe la característica o atributo que se mide.

Diseño de Experimento

La necesidad de poseer datos  sobre la población y sus condiciones materiales de existencia se han sentido  desde que se establecieron sociedades humanas organizadas.

Vamos a exponer de forma sencilla una serie de definiciones

Muestra-  Todo subconjunto representativo de la población, de forma que las conclusiones sacadas en aquella se generalizan a esta.  Al número de elementos o individuos de una muestra se llama tamaño de la muestra. Muestreo es seleccionar una muestra de la población.

Población - Universo colectivo, cualquier conjunto de personas, objetos, animales, plantas, instituciones, entes en general que son portadores de una serie de características.  A cada elemento de la población se le llama Individuo (por su origen demográfico) o unidad estadística

Muestra aleatoria simple-  Se hace haciendo uso de una tabla de números aleatorios, que se construye en forma tal que genere series de números aleatorios para que se produzca una muestra imparcial.

Variación-  Es una medida de dispersión estadística, haciendo un promedio de la distancia ajustada de sus valores posibles del valor previsto.  La positiva raíz cuadrada de la variación, llamada desviación de estándar, tiene las mismas unidades que las variables originales y puede ser más fácil de interpretar por esta razón.

Ejemplo: Usa el muestreo para predecir

Una tienda de animales envió una encuesta por correo a los residentes para determinar sus mascotas favoritas. Cincuenta personas respondieron y los resultados se muestran en la tabla.

¿Es válido este método de muestreo? De ser así, ¿cuantas personas esperas que elijan a los perros como mascota favorita en una ciudad de 1585 habitantes? Explica.

Esta es una muestra sesgada y de respuesta voluntaria ya que sólo  incluye a aquellos que quieran participar en la encuesta. Por lo tanto, este método de muestreo no producirá una predicción  valida del número total de perros en la ciudad.

Ejemplo 2:

De un lote de 7500 chips de computadora producidos, el fabricante hizo un muestreo de cada 150 chips al azar y encontró que 2 eran defectuosos.  ¿Es válido este método de muestreo? De ser así, calcula cuantos de los 7500 chips esperarías que sean defectuosos. Explica.

Esta es una muestra aleatoria sistemática porque las muestras se eligen según un intervalo específico. Por lo tanto, este método de muestreo es razonable y producirá una predicción válida.  Como se hizo un muestreo de 150 chips, había un total de 7500  dividido 150 ó 50 chips al que se les hizo un muestreo y 2 estaban defectuosos. Dos de un total de 50 ó  4% tenían defectos. Por 10 tanto, calcula e14% de 7500.

 Análisis de Datos

Las medidas de Tendencia Central, nos sirven para representar con un solo número todo un conjunto de datos. Se conocen como medidas de posición.  La más conocida, es la media llamada con más propiedad Media Aritmética (en la práctica cotidiana se conoce simplemente como el promedio). También se emplean con frecuencia la Mediana y la Moda.

Medidas de Tendencia Central

¿Por qué usar Medidas de Tendencia Central?

El propósito de las medidas de tendencia central es:

Ø  Mostrar en qué lugar se ubica la persona promedio o típica del grupo.

Ø  Sirve como un método para comparar o interpretar cualquier puntuación en relación con la puntuación central o típica.

Media aritmética

La media aritmética es probablemente la medida de tendencia central más importante. También se le llama promedio y la vemos aplicada a diario en casi todos los espacios y medio dedicados a brindar información.

x  =  S X

           n   

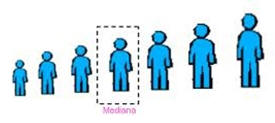
Mediana

La mediana es la observación central de los valores de una población o muestra una vez que éstos han sido ordenados de forma ascendente o descendente. Para un número par de observaciones, la mediana es el promedio de los dos valores intermedios.

Moda

La moda es el valor que aparece con más frecuencia en un conjunto de datos.

Medidas de Dispersión

Varianza

En términos conceptuales la varianza es la media aritmética de las desviaciones de la media elevadas al cuadrado. Las fórmulas para calcular cada una son como sigue:

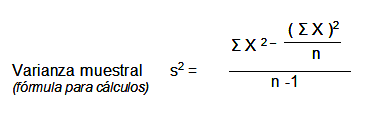
Desviación estándar

Resulta obvio pensar que al calcular la raíz cuadrada de la varianza obtendremos valores expresados en la misma unidad de medida de que los datos que nos interesan. Uno definición formal de la desviación estándar es la raíz cuadrada positiva de la varianza.

 La desviación estándar es un promedio de las desviaciones individuales de cada observación con respecto a la media de una distribución.  

Las fórmulas que se utilizan para calcularla se pueden simplificar entonces en las siguientes expresiones:

Amplitud

La amplitud no toma en consideración el número de observaciones de la muestra estadística, sino solamente la observación del valor máximo y la del valor mínimo.

Amplitud de clase. Se considera la amplitud que deben tener las clases consideradas para realizar un estudio estadístico. Para n datos con k clases se determina que la amplitud de clase.

La palabra datos significa hechos o números que describen algo. Un conjunto de datos es más fácil de entender cuando está organizado en una tabla o gráfica. No hay una manera óptima de organizar datos, pero hay muchos métodos buenos.

Ejemplos:

Los datos para los perímetros de los rectángulos siguientes aparecen debajo de las figuras:

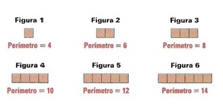
 El patrón de los perímetros es más fácil de ver si organizas los datos en una tabla. Cada perímetro es 2 más que el anterior.

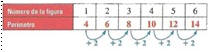
Tablas

¿Has visto alguna vez un partido de béisbol en un campo que no tiene marcador? Es difícil saber cuántas carreras han anotado. EI marcador es un tipo de tabla. Las tablas se usan para organizar la información, y son particularmente útiles para resolver problemas que requieren de varios pasos.

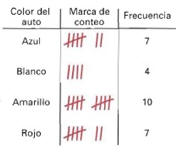
 Una tabla de frecuencia contiene diferentes  categorías, marcas de conteo y la frecuencia de aparición de cada elemento.   Esta tabla de frecuencia muestra los colores de auto en un estacionamiento. Las marcas de conteo se usan para contar el número de automóviles.  

Gráficas

Tipos de Gráficas

Las gráficas representan y comparan datos visualmente de diferentes fuentes.  Muestran los cambios a lo largo de un periodo y pueden hacer predicciones  del futuro.

Tareas

Portafolio

Diario Reflexivo

 1- Cuando se suman todas las puntuaciones de una prueba y luego se divide el resultado por el número total de las    puntuaciones obtenemos la:

   a. media

   b. mediana

   c. moda

   d. desviación estándar

 2. Es el valor de un dato que aparece con mayor frecuencia en  un grupo de   datos:

    a. la mediana

    b. la desviación estándar

    c. la moda

    d. la media

3- Indique cual es la media en la siguiente distribución; 10, 5, 15, 10, 20, 22, 9, 5, 15 y 19:

  a.15

  b.13

   c.10

   d. 20

4. Indique cual es la mediana en la siguiente distribución; 20, 15, 10, 5 y 12:

  a. 10

  b. 15

  c.  5

  d. 12

5.  Es la medida de tendencia central que divide los datos   por la misma mitad:

  a. la mediana

  b. la media

  c. la moda

 d. la desviación estándar

 6. ¿Cuál sería la medida más apropiada para describir el promedio de los datos siguientes; 50, 60, 40, 30, 20, 10 y 15:

  a. la desviación estándar

  b. la moda

  c. la media

 d. la mediana

7. Es uno de los requisitos para calcular la mediana:

  a. sumar los valores de los datos

  b. ordenar los datos

  c. buscar el promedio

 e. identificar el dato de mayor frecuencia

Solución

1-      a

2-      c

3-      b

4-      d

5-      a

6-      c

7-      b

1- ¿Cuál es la media aritmética en madurez lectora de un grupo de 6 alumnos de preescolar que siguieron un método de enseñanza de la lectura de tipo comprensivo? ¿Y la de aquellos seis alumnos que no asistieron a preescolar? Justifica la respuesta sabiendo que el intervalo de puntuaciones fluctúa entre 0 y 20.

Puntuaciones del grupo 1: 18, 17, 7, 12, 15, 6

Puntuaciones del grupo 2: 7, 10, 9, 4, 2, 7

2- ¿Cuál es la moda y mediana de la muestra  del ejercicio 1?

3-    Se tiene una muestra de tamaño 6 con valores de datos 10, 18, 12, 17,15 y 12. Calcule la media, la moda y la mediana.

Solución

1- Media - Grupo 1-   12.5

     Media Grupo 2-  6.5

2- Moda-  Grupo 1- No hay

                  Grupo 2 -  7

     Mediana- Grupo 1- 13.5 

                     Grupo 2 – 7.5

3-Mediana = 13.5

    Moda = 12

1-Calcular la desviación estándar de la distribución:

9, 3, 8, 8, 9, 8, 9, 18   

2-Calcular la varianza de la distribución

9, 3, 8, 8, 9, 8, 9, 18

 3-Calcular la varianza  y la desviación estándar

9, 25, 9, 36, 16, 4, 64, 9, 49, 25, 64, 81, 16, 25, 25, 9

Solución

             1-

2-      Desviación estándar = 3.87

3-      Varianza= 15

4-      Varianza 4.125      DS=  2.03

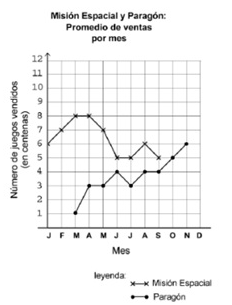
1. Identifica que tipo de gráfica
2. ¿Qué muestra la gráfica?
3.  ¿Qué juego tiene el mayor número de ventas para cualquier mes?
4.  ¿Qué mes muestra la mayor diferencia en ventas entre Misión Espacial y Parragón?
5. ¿Cuál de los dos juegos tiene el mayor alcance en el número promedio de unidades vendidas?
6. ¿Cómo se identifica el eje horizontal?
7. Esta gráfica circular representa el uso de internet en 1996.
8.  ¿Qué sector compone 66% de los usuarios de internet?
9. ¿Qué por ciento de usuarios son Del hogar?
10. Los negocios, educación y gobierno, ¿componen más del 80% de los usuarios?

2- Se tiró un cubo numérico 10 veces. Presenta los datos en una tabla de frecuencia y construye una gráfica de barras para representar los datos.

5, 2,  5,  4, 1,  6, 5,  2,5, 1

© Derechos Reservados

Escuela Virtual de Educación Acelerada Proyecto Salón Hogar Inc.