MATEMÁTICAS INTEGRADAS 2

Patrones, Sucesiones y Series

Módulo 3

Patrones, Sucesiones y Series

 En la vida diaria se determinan razones de cambio de diversas situaciones de tipo

Natural, Económico, Social.  En la naturaleza abundan las sucesiones y series; por ejemplo, la sucesión de Fibonacci está escondida en la intrincada del caracol de un nautilo.

Toda secuencia ordenada de números reales recibe el nombre de sucesión. Dentro del grupo de sucesiones existen dos particularmente interesantes por el principio de regularidad que permite sistematizar la definición de sus propiedades: las progresiones aritméticas y geométricas

Patrones;

Cosas que están ordenadas siguiendo una o varias reglas.

Ejemplo: hay un patrón en estos números: 2, 7, 12, 17, 22, ... La regla es "empieza en 2 y suma 5 cada vez"

Se conoce como razón de cambio a la medida en que una variable cambia con respecto a otra, como por ejemplo la velocidad, la cual es una razón de cambio del espacio con respecto al tiempo (lima dx/dt, cuando t tiende a cero)

Una sucesión  aritmética es una serie de números tales que la diferencia de dos términos sucesivos cualesquiera de la secuencia es una constante, cantidad llamada diferencia de la progresión o simplemente diferencia o incluso "distancia".

Ejemplo, la sucesión 3, 5, 7, 9, 11,... es una progresión aritmética de constante (o diferencia común) 2.

Una sucesión geométrica está constituida por una secuencia de elementos en la que cada uno de ellos se obtiene multiplicando el anterior por una constante denominada razón o factor de la progresión.  y el término que le precede es una cantidad fija llamada razón.

Ejemplo: la secuencia de números 2, 4, 8, 16, 32, 64, 128 es una progresión geométrica con razón 2;

Formula Generales  para Secuencias Aritméticas

Formula Generales  para Secuencias Geométricas

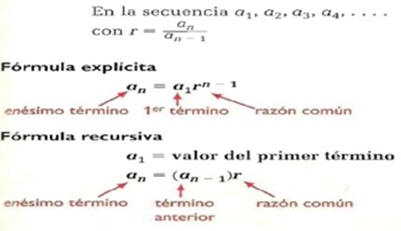
Ejemplo:

 Halla el noveno término de la secuencia geométrica -2, 6, -18,54, ....

Ejemplo

Decide si cada secuencia es aritmética, geométrica o ninguna de las dos.

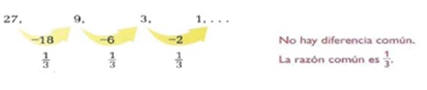
Es una secuencia geométrica

Términos Generales

Una sucesión queda bien determinada siempre que sean conocidos los primeros términos y la ley por la cual pueden obtenerse nuevos términos, o bien, a través de la propiedad que caracteriza a cada uno de sus términos.

Mediante una expresión analítica, o fórmula del término gene­ral, ya que en estos casos basta con ir dando valores al contador del término general para ir obteniendo todos y cada uno de los términos de la sucesión.  Mediante una ley de recurrencia, es decir, una relación entre un térmi­no cualquiera y los anteriores, o entre un término, los anteriores y el lugar que éste ocupa,

Una de la más conocida es la  sucesión de Fibonacci. Esta estructura es conocida como triángulo de Pascal o triángulo de Tartaglia, y las suce­siones que con él se forman son de lo más variopinto, la propia de Fibona­cci se encuentra dentro de esta estructura.

Hay un tipo de sucesiones, llamadas progresiones, en las que esto último es relativamente sencillo. Progresiones, son un caso particular de sucesiones en las que la ley de for­mación de términos, y otra serie de características, las hacen interesantes de anali­zar. Hay dos tipos, o clases, de progresiones que merece la pena estudiar en  Se llama término general a la regla que sigue a la sucesión.

Término general de Progresiones Aritméticas: es aquel en el que se obtiene cualquier término sumándole la diferencia al término anterior. El término de una progresión aritmética es la expresión que nos da cualquiera de sus términos, conocidos alguno de ellos y la diferencia de la progresión.  Siguiendo el principio o ley de inducción, llegaríamos a que en el caso general , que es el término general.

Fórmula Suma de una Serie Aritmética:

 Una serie puede escribirse de manera compacta usando notación sigma. La notación sigma usa el signa de suma 1, que es la le S griega sigma.

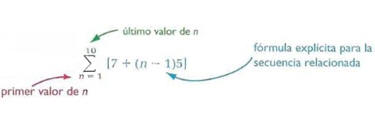
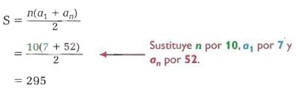
Ejemplo: Suma de una Progresión Aritmética

 Halla el número de términos de la serie.

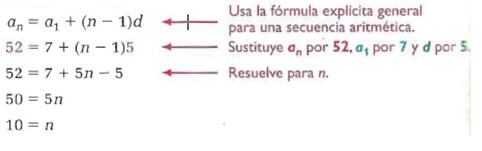
Ejemplo: Suma de una Progresión Aritmética

 Usa la fórmula para la suma de una serie aritmética finita.

Término general de Progresiones Geométricas: siguiendo el principio o ley de inducción, llegaríamos a que en el caso general , que es el término general.

 Fórmula Suma S de una Serie Geométrica finita con n términos y razón común r:

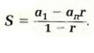
Suma de una Serle Geométrica Infinita

La fórmula general para la suma S de una serie geométrica infinita es.

 Ejemplo: Suma Sucesiones Geométrica

 Halla la suma de la serie (-1) + 3 + (-9) + 27 + '" + 2187.

 Usa la fórmula para la suma de una serie geométrica finita.

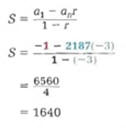
Ejemplo: Suma Sucesiones Geométrica Infinitas

Decide si la serie           tiene una suma.

La serie es geométrica con tiene una suma                     

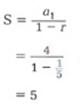
 La suma de la serie es 5.

Relaciones de recurrencia

En nuestra vida cotidiana son frecuentes las relaciones de todo tipo: "madre-hijo”, “profesor-alumno", "empleado-jefe”,"paciente-médico", etc.  En matemática, esta palabra "relación" es usada en forma semejante pero es preciso indicar la conexión entre los dos elementos como en: "a igual b", "x menor que y", "v doble de u" que se escribe simbólicamente por: "a = b", "x < y" "v = 2u".

Ejemplo:

Para a = b se tienen (3, 3), (2,2), (2/3, 2/3), (π, π), (0.02, 0.02),...

Para x < y se tienen (2, 5), (3,0), (2, π), (24,8), (0.3, 0.31),...

Para v = 2u se tienen (1, 2), (3, 23), (0.001, 0.002), (2,1), (π,2π),

Una relación de recurrencia para una sucesión  es una fórmula que expresa cada término a partir de cierto, en función de uno o más de los términos que le preceden. Los valores de los términos necesarios para empezar a calcular se llaman condiciones iniciales. Se dice que una sucesión es una solución de la relación de recurrencia si su término general verifica dicha relación.

Relaciones de recurrencia lineales homogéneas

Definición

Llamaremos ecuación característica de la relación de recurrencia  a la ecuación.  A sus valores de solución se les llama raíces características.

Ejemplo: Formula explícita para la secuencia de Fibonacci

Relaciones de recurrencia lineales no homogéneas

Pasos para resolver una relación de recurrencia lineal no homogénea

-Se obtiene la solución general de la ecuación homogénea asociada.

Se obtiene una solución particular de la relación de recurrencia no homogénea.

La suma de la solución general de la ecuación lineal homogénea asociada y de una solución particular

de la relación de recurrencia lineal no homogénea nos da la solución general de la relación de

recurrencia lineal no homogénea. La solución específica se obtiene a partir de las condiciones iniciales.

Ejemplo:

Ejemplo: Los conejos y la secuencia de Fibonacci

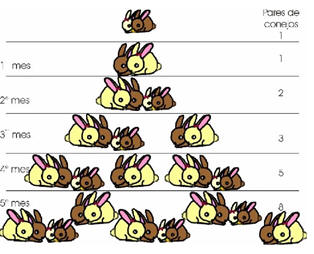
                 1- Usa el patrón para escribir los tres números siguientes.

                  2. Haz una tabla en la que muestres la cantidad de cuadrados de cada figura. Luego indica cuántos cuadrados hay en la quinta figura del patrón. Usa dibujos para justificar tu respuesta.

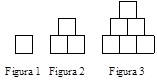
                  3- Usa el patrón para dibujar las tres figuras siguientes.

4- Decide si la secuencia es aritmética, geométrica o ninguna de las dos.

a)      1, 3, 7, 15,....

b)      2- 12, 9.5, 7,  4.5,....

c)      5,  8,  11,  14,....

5. Evalúa

6. Halla la suma de la serie aritmética

a)      98+ 94 + 90 + 86 + ... + 6

7. Cuáles de las siguientes secuencias {a_n} son soluciones de la relación de recurrencia

a_n=8a_n-1-16a_n-2 ?

Contestación

1-       El patrón consiste en restar 13.

2-

3- El patrón consiste en triángulos rectángulos que giran en sentido contrario a las manecillas del reloj.

4- Contestación

a)        Ninguna

b)       Aritmética

c)        Aritmética

 5- a.  32 

6...  1248   

7.   a.  No   b. no  c. si    d.  Si

© Derechos Reservados

Escuela Virtual de Educación Acelerada Proyecto Salón Hogar Inc.