MATEMÁTICAS INTEGRADAS 3

 Función Polinómicas y Racional

Módulo 2

GRADO 12

Funciones Polinómicas

Una función polinómica se escribe de la forma:
donde son    números reales y n es un entero no negativo (positivo o cero). El dominio de esta función consiste de todos los números reales.

Ejemplo:

Grado del polinomio

El grado del polinomio es el número correspondiente a la potencia más alta de x’s.

Ejemplo:

X²+3x+1    Grado 2

X³2      Grado 3

Ejemplo:

Determine cuáles de los siguientes son polinomios. En aquellos que lo sean, diga su grado.

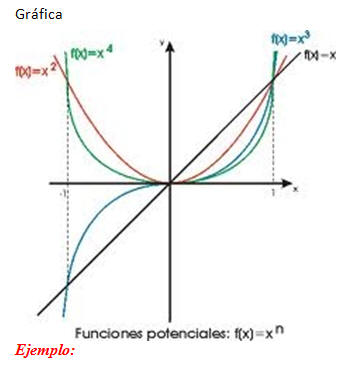
Funciones potencia

Una función potencia tiene la forma  donde a es un número real distinto de cero y n es un entero positivo. Cuando el exponente es 1, llamamos a la función lineal.

Si la función tiene un grado que es par:

v  Es simétrica con respecto al eje y.

v  Su dominio es los reales.

v  Su campo de valores son los reales no negativos.

v  Su gráfica contiene los puntos (0, 0) ; (1, 1) ; y (1,1).

v  Si la potencia aumenta en magnitud, la gráfica crece rápidamente a medida que x aumenta, pero para x cerca del origen, la gráfica tiende a aplastarse y acercarse al eje de x.

Ejemplo:

Observa que esta gráfica tiene su vértice en el origen y abre hacia arriba.  El dominio de f(x) es el conjunto de todos los números reales y  el recorrido es el conjunto de los números reales no negativos. La función es par y tiene simetría al eje de y.

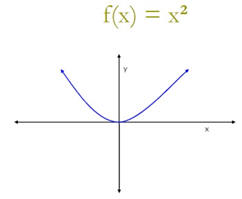
Si el grado de la función es impar:

•   Hay simetría con respecto al origen.

•   Su dominio es los reales.

•   Su campo de valores también.

•   La gráfica siempre contiene los puntos (0, 0) ; (1, 1) ; y (1,1).

•   A medida que aumenta la potencia, la gráfica se hace más vertical cuando x> 1 ó x< 1,

•   pero para 1 < x< 1, las gráficas tienden a acostarse y acercarse al eje de x’s.

Ejemplo:

Como puedes observar en esta gráfica, tanto el dominio como el recorrido de la función f(x) = x³ es el conjunto de los números reales.  La gráfica pasa por el origen y es simétrica al origen.

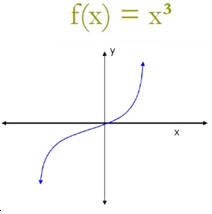
Teorema Fundamental Del Álgebra

El teorema fundamental del álgebra establece que: todo polinomio en una variable de grado n ≥ 1 con coeficientes reales o complejos tiene por lo menos una raíz (real o compleja).  

Supongamos que tenemos una ecuación de la forma f(x) = 0. Llamaremos raíz de dicha ecuación a cualquier número n que verifique f(n)=0. A n también se le llama cero de la función f. Diremos que una ecuación tiene raíces separadas, si para cada raíz existe un intervalo que no contiene otras raíces de la ecuación.

El cálculo aproximado de raíces de una ecuación se hace, por lo general, en dos etapas:

v  Separación de raíces.

v  Obtención de una aproximación tan cercana como quiera.

Considérese el polinomio:

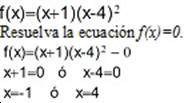
Si f es una función polinómica, y r es un número real, para el cuál f(r) = 0, entonces a r se le llama un cero real de f, o raíz de f.  Si r es un cero real de f, entonces:

v  (r, 0) es un intercepto en x en f.

v  (xr)  es un factor de f.

Ejemplo:

Halle los ceros reales y la multiplicidad de la siguiente función.

x= 3 es un cero de multiplicidad 2.

x= 7 es un cero de multiplicidad 1.

x= 1/2 es un cero de multiplicidad 5.

Ejemplo:

Halle los intercepto en x y y de f.  Los intercepto en x (ceros) son (1, 0), (5,0), y (4,0)

Para hallarlos en y, evalúe f (0).  Por lo tanto, el intercepto en y es (0,20)

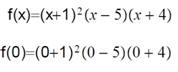
Ejemplo:

Determine si la gráfica cruza o toca el eje de x en cada intercepto.

v  x = 4  es un cero de multiplicidad 1 (cruza el eje x) 

v  x = -1 es un cero de multiplicidad 2 (toca el eje x’s)

v  x = 5 es un cero de multiplicidad 1 (cruza el eje x’s

División Sintética

La división sintética es un procedimiento matemático para dividir polinomios por binomios de la forma x – c donde c es una constante. Es una manera corta de obtener el cociente y el residuo de la división de un polinomio cualquiera p(x) entre otro polinomio de la forma g(x) = xc. En esta forma de división solo se trabaja con los coeficientes del polinomio p(x).

Use división sintética para hallar el cociente y el residuo si:

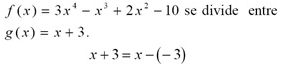
Como ves, los números que resultan son los coeficientes del polinomio resultante o cociente. Recuerda que este polinomio tiene un grado menos que el polinomio original. De ahí que el resultado sea el que observas.

Ejemplos: Use la división sintética

1.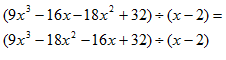

 2 |  9   -18   -16   32

                9     18       0    -32

                9       0     -16     0  residuo

Resultado:

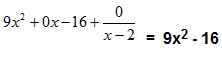2.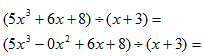

3 |  5      0       6        8

               -15     45     -153

       5      -15     51     -145

Resultado:   

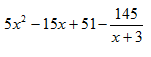
Teorema del Residuo

Si una función polinómica f(x) se divide por un binomio de la forma x –c, el resido será f(c).

Demostración: Usando el Teorema de División, con g(x) = (x - c), tenemos:

Evaluando en x = c se obtiene el resultado deseado.

Aplicación:

Crea una gráfica para un pronóstico del tiempo de cinco días para una ciudad de Puerto Rico en donde el aumento de las temperaturas es constante y se usan para predecir la máxima del día. Identifica el lugar que utilizaste para recopilar tus datos e incluye los datos para las lecturas de temperatura y la hora del día que las lecturas fueron tomadas. Nombra los ejes.

Lugar: __________________________________________________________

1. Usa tu gráfica para contestar las siguientes preguntas.

2. La gráfica es una representación de una _________

3. ¿Es la gráfica una función polinómica o cuadrática._______________

4. Identifica el intercepto en y _______________

5. Identifica los valores a lo largo de cada eje. _______________

6. Escribe un párrafo que describa las características de tu gráfica en_______________________

7. Describe las características de una gráfica de temperatura en la cual los puntos están en más de un cuadrante. _______.

Solución: respuestas varían de acuerdo a la información

 Funciones Racionales

Donde p y q son funciones polinomiales y q es diferente de 0. Su dominio son los números reales para los cuales q es distinto de 0. Para dos polinomios cualquiera, A y B, su fracción es conocida cono una función racional.

Dominio

El dominio de las funciones racionales es el conjunto de todos los números reales tal que el denominador sea diferente de cero.

En su dominio de definición, las funciones racionales son continuas e indefinidamente derivables.

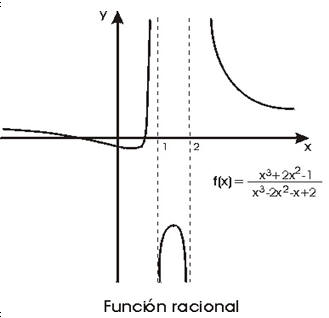
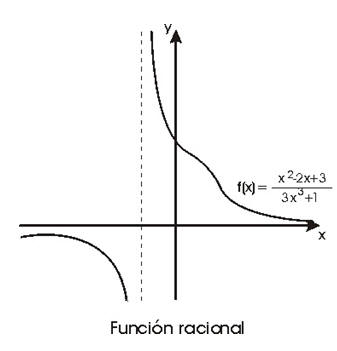
Tendencia en las funciones racionales

Cuando el grado del numerador es menor que el grado del denominador.

Ejemplo:

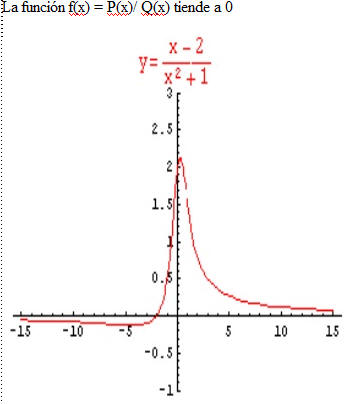
Asíntotas y Gráficas

Para analizar una función racional debemos tener en cuenta las siguientes características observables:

El dominio está formado por los valores de R

Es una recta a la cuál tiende a acercarse la función pero en la mayoría de los casos no la corta ni la toca. Existen asíntotas horizontales, verticales y oblicuas. Asíntota Horizontal es una recta horizontal a la que tiende a acercarse la función. Cada vez que la variable independiente (x) adquiere o toma valores más grandes y la variable dependiente (y) tiende a acercarse a un número, podemos decir que existe una asíntota horizontal en dicho número. Asíntota Vertical es una recta vertical a la que tiende a acercarse la función. Cuando la variable independiente tiende a acercarse a un número por derecha o por izquierda, es decir con valores mayores y con valores menores a dicho número, y la variable dependiente tiende a tomar valores muy grandes o muy pequeños, se dice que hay una asíntota vertical.

Ejemplo:

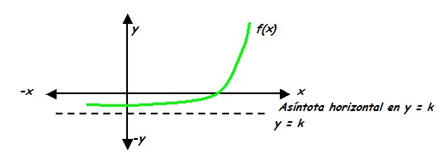
Halle el dominio de las siguientes funciones racionales.

Ejemplo:

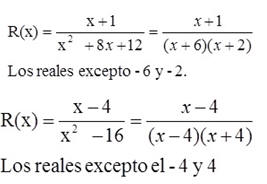
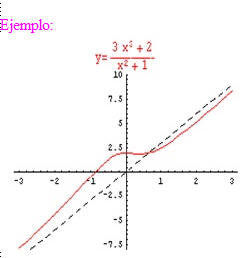
Aplicaciones:

1. ¿Cuál es la diferencia entre la función polinómica: f (x) = x + 4 y la función racional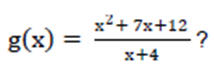

A. g(x) no tiene intercepto con el eje de y.

B. f(x) no tiene un límite máximo.

C. f(x) es una recta y g(x) es una curva.

D. g(x) no está definida en un punto.

2. Encuentra todas las asíntotas verticales, horizontales y oblicuas de las siguientes funciones. No traces la gráfica.

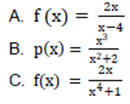
Solución:

1. d

2. a) asíntota vertical: x = 4

b) asíntota vertical: no hay

c) asíntota vertical: no hay

a) Asíntota horizontal: y = 2

b) asíntota horizontal: no hay

c) asíntota horizontal: y = 0

a) asíntota oblicua: no hay

b) asíntota oblicua: y = x

© Derechos Reservados

Escuela Virtual de Educación Acelerada Proyecto Salón Hogar Inc.