|
MATEMÁTICAS INTEGRADAS 3
Función Exponencial

Módulo 3
GRADO 12
Función Exponencial
Se llaman funciones exponenciales a todas aquellas funciones de la forma f(x) = bx, en donde la base b, es una constante y el exponente la variable independiente. Estas funciones tienen gran aplicación en campos muy diversos como la biología, administración, economía, química, física e ingeniería.
La definición de función exponencial exige que la base sea siempre positiva y diferente de uno (b>0 y b≠1). La condición que b sea diferente de uno se impone, debido a que al reemplazar a b por 1, la función bx se transforma en la función constante f(x) = 1. La base no puede ser negativa porque funciones de la forma f(x)=(-9)1/2 no tendrían sentido en los números reales.
El dominio de la función exponencial está formada por el conjunto de los números reales y su recorrido está representado por el conjunto de los números positivos.
Resumen de las características de
![]()
Dominio: Los Reales
Rango: (0, )
No tiene intercepto en x
Intercepto en y: (0,1)
Asíntota horizontal: y = 0 cuando x es infinito
Es creciente
Es uno-uno
La gráfica de una función exponencial se puede obtener como sigue:
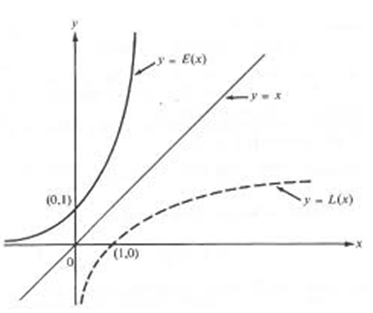
Ejemplo:
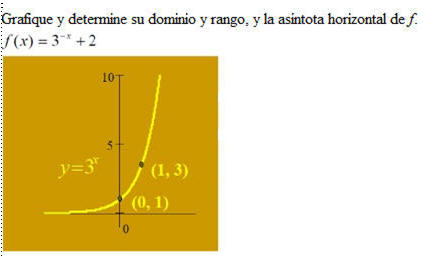
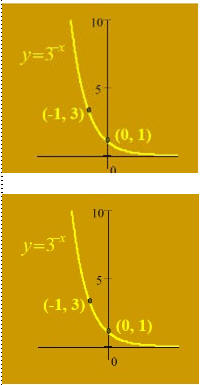
Definición de función creciente y Decreciente
Una función y = f (x) se llama función creciente si y aumenta (algebraicamente) cuando x aumenta. Una función y = f(x) se llama función decreciente si y disminuye (algebraicamente) cuando x aumenta. La gráfica de una función indica claramente si es creciente o decreciente.
Ejemplo
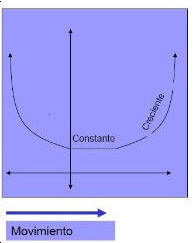
Al variar un punto a lo largo de la curva de izquierda a derecha, la curva, es decir, a medida que la x del punto aumenta. La función (= y) aumenta. Evidentemente, Ay y Ax tienen un mismo signo.
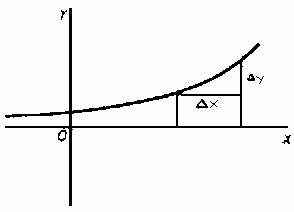
Ejemplo:
Si observamos la función que está ilustrada y vemos su movimiento de izquierda a derecha, podemos ver que la función decrece, luego se hace constante y después creciente.
Ejemplo:
La función f(x) = 2x + 4 es una función creciente en los números reales.
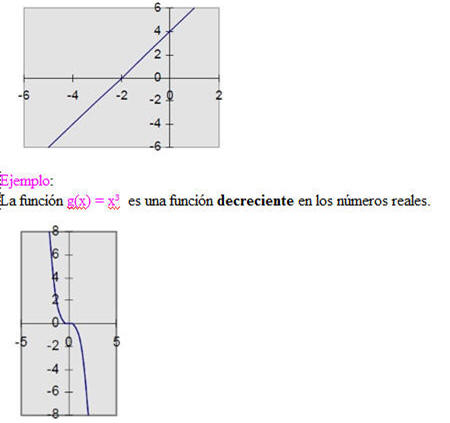
Ejemplo:
La función f(x) = x² es una función decreciente en el intervalo de menos infinito a cero y creciente en el intervalo de cero a infinito.
Uso en la vida diaria
Las funciones exponenciales se usan para describir situaciones de la vida real. Henri Becquerel descubrió que los fósiles contienen, en forma natural, átomos radiactivos de carbono-14. Cuando el organismo muere la cantidad de carbono-14 presente comienza a desintegrarse, y podemos saber la edad del fósil. Desde el punto de vista de la matemática de un hecho o fenómeno del mundo real, las ecuaciones exponenciales se usan desde el tamaño de la población hasta fenómenos físicos como la aceleración, velocidad y densidad. Se usan igual para dar el crecimiento de cosas como: el crecimiento de una población determinada, el crecimiento de personas infectadas con el VIH (sida), o la disminución de una carga de la carga de un condensador, inundaciones de tiendas agrícolas, vida media de una sustancia radioactiva, desintegración atomiza, etc.
Aplicaciones de las ecuaciones exponenciales.
Aplicación química- Se sabe que la masa de cierto material radioactivo disminuye en función del tiempo (t) según la función m(t)= 60 . 2-5.t estando m en gramos y t en horas. ¿Después de cuánto tiempo la masa del material es de 30 gramos?
Aplicación en economía - Se calcula que el monto del capital, en millones de pesos, que tiene depositado un señor en el banco, en cualquier momento (t) meses puede ser calculado mediante la función f(t) = 7,5 . 1,02t . Función: C = C0 ( ½ ) kt, donde C0 es la cantidad inicial de carbono, t es. El número de años que pasan. si la vida media del carbono 14 es 5730 años
Aplicaciones en la vida Investigaciones policiales: - Una persona es encontrada Muerta en su Departamento, la Brigada de Homicidios llego a las 10 de la noche, los datos recogidos por los Detectives fueron temperatura de la habitación 21ºC (A) , la temperatura del cadáver al ser encontrado fue de 29ºC y una hora después era 28ºC .Considerando la función: T(t) = A + (B – A ) e –kt . Calcular el valor de K si t = 1 Con el dato anterior Determine la hora en que fue encontrado el cuerpo Inerte si este tenía una temperatura de 37ºC cuando estaba vivo.
Aplicaciones en la vida diaria Caso heroico: - Un joven muy valiente arriesga su vida por salvar a un niño. La radio informa después de una hora el 25% de la población escucha la noticia, Si el porcentaje de personas que escucha sigue el modelo exponencial: F(t) = N ( 1 – 10-kt ), k se expresa en porcentaje, t en segundos . Determinar cuánto tiempo trascurre para que el 90% de la población sepa la noticia
Aplicaciones en Medicina - El contenido en gramos de un medicamento en el organismo humano, después de t horas de ingerido, se modela de acuerdo a la ecuación: y = 100x5-0,5t , t ≥ 0. ¿Después de cuántas horas de ingerido el medicamento quedan 20 miligramos en él organismo?. ¿Cuántos miligramos de medicamento quedan en el organismo después de 4 horas de ingerido?
Las funciones exponenciales son las que tienen más presencia en los fenómenos observables, por lo que existen diversidad de situaciones cuyo estudio implica el planteamiento de ecuaciones exponenciales o logarítmicas.
Ejemplo de ello es la escala Rither.
Función logarítmica
Como la exponencial, la función logarítmica se utiliza con asiduidad en los cálculos y desarrollos de las matemáticas, las ciencias naturales y las ciencias sociales. Entre otros fines, se usa ampliamente para «comprimir» la escala de medida de magnitudes cuyo crecimiento, demasiado rápido, dificulta su representación visual o la sistematización del fenómeno que representa.
Definición de función logarítmica
Una función logarítmica es aquella que genéricamente se expresa como f (x) == logax, siendo a la base de esta función, que ha de ser positiva y distinta de 1.
Nota: La notación log b y = x se lee “el logaritmo de y en la base b es x”.
Propiedades de la función logarítmica
Las propiedades generales de la función logarítmica se deducen a partir de las de:
v La función logarítmica sólo existe para valores de x positivos, sin incluir el cero. Por tanto, su dominio es el intervalo.
v Las imágenes obtenidas de la aplicación de una función logarítmica corresponden a cualquier elemento del conjunto de los números reales,
luego el recorrido de esta función es R.
v En el punto x = 1, la función logarítmica se anula, ya que loga 1 = 0, en cualquier base. La función logarítmica de la base es siempre igual a 1.
v Finalmente, la función logarítmica es continua, y es creciente para a > 1 y decreciente para a < 1.
Ejemplos:
¿A qué exponente hay que elevar la base 5 para obtener 25? Al exponente 2, ya que 52 = 25.
Decimos que “el logaritmo de 25 en la base 5 es 2”. Simbólicamente lo expresamos de la forma
![]()
| De manera que, |
|
es equivalente a |
|
(Observa que un logaritmo es un exponente.) |
Nota: El dominio de una función logaritmo es el conjunto de todos los números reales positivos y el recorrido el conjunto de todos los números reales.
De manera que, log10 3 está definido, pero el log10 0 y log10 (-5) no lo están. Esto es, 3 es un valor del dominio logarítmico, pero 0 y -5 no lo son.
Propiedades de las funciones logarítmicas:

Ejemplo
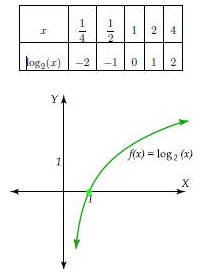
Considere las funciones logarítmicas f(x) = log2 x, construye la gráfica.
Solución
Para realizar la gráfica de f y g debemos construir para cada una de ellas, una tabla de valores conveniente de la manera siguiente
Aplicación
1.¿A qué familia de funciones pertenece la función representada en la siguiente gráfica?
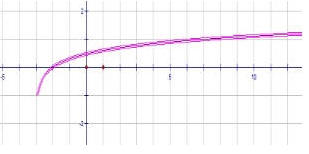
A. Funciones Exponenciales
B. Funciones Logarítmicas
C. Funciones Trigonométricas
D. Funciones Definida por partes
2. ¿Qué podemos decir de la función logarítmica y la función exponencial?
A. La función logarítmica es la inversa de la función exponencial.
B. La función logarítmica es lo mismo que la función exponencial.
C. La función logarítmica tiene exponente y la función exponencial tiene logaritmos.
D. Las funciones no se puede comparar.
3. Si logb 3 = 1.10 y logb 7 = 1.95 , entonces logb 21 = _______.
A) 0.85
B) 3.05
C) 2.145
D) 2.85
4.En la ecuación log3 81 = x, el valor de x es:
A) 2
B) 3
C) 4
D) 9
Soluciones
1.b
2.a
3.b
4.c
Aplicaciones
Asignación: Valor 50 pts. Contesta las preguntas
1- ¿Qué podemos decir de la función logarítmica y la función exponencial?
A. La función logarítmica es la inversa de la función exponencial.
B. La función logarítmica es lo mismo que la función exponencial.
C. La función logarítmica tiene exponente y la función exponencial tiene logaritmos.
D. Las funciones no se puede comparar.
2. ¿A qué familia de
funciones pertenece la función representada en la siguiente
gráfica? 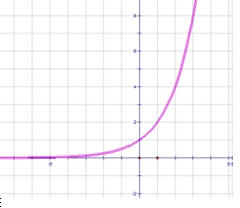
A. Funciones Exponenciales
B. Funciones Logarítmicas
C. Funciones Trigonométricas
D. Funciones Definidas por partes
3. La función f(x) = 3x+2, es una función:
A. Logarítmica
B. Trigonométrica
C. Exponencial
D. Racional
4. La solución de la ecuación 2x =6 expresada a dos lugares decimales es:
A) x=0.39
B) x =2.00
C) x = 2.58
D) x = 3.00
5. Observa la gráfica 1 y la gráfica 2. La gráfica 2 evidencia el desplazamiento. ¿Cuántas unidades se desplazó hacia abajo?
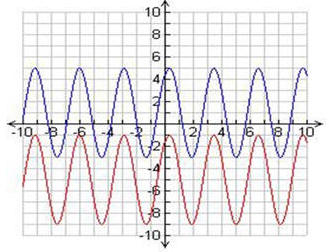
6. Observa la siguiente gráfica que representa los volúmenes pulmonares. El tidal volume significa la respiración normal.
¿Cuántos litros de aire se mueven aproximadamente en la respiración normal de acuerdo a la gráfica
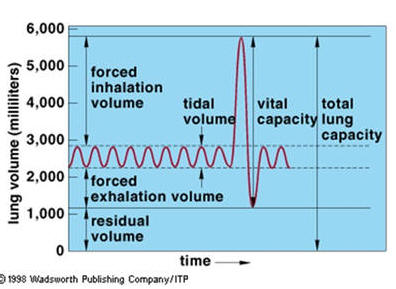
A. 3 litros
B. 2 litros
C. 1 litro
D. 0.5 litro
7. Observa la siguiente gráfica que representa el mecanismo de la respiración normal. ¿Cuántos litros de aire se mueven en la respiración?
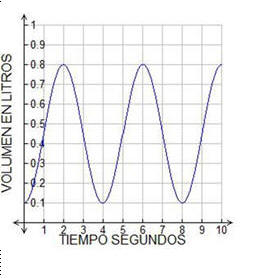
A. 0.10
B. 0.35
C. 0.70
D. 0.90
Solución
1.a
2.a
3.c
4.c
5. 6
6.c
7.c
© Derechos Reservados
Escuela Virtual de Educación Acelerada Proyecto Salón Hogar Inc.
|
