MATEMÁTICAS INTEGRADAS 4

Las Funciones Trigonométricas Clásicas

Modulo 2

GRADO 12

Las Funciones Trigonométricas Clásicas

Dos triángulos que tengan un ángulo agudo congruente son semejantes por definición.  Por lo tanto sus lados correspondientes son proporcionales entre sí.

Esto es

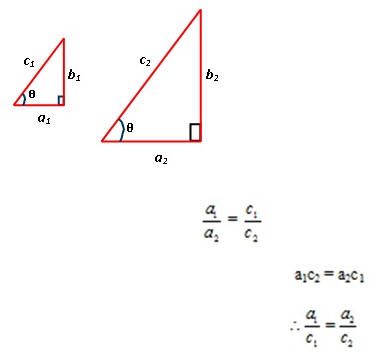
Observa que:

a₁ = medida del lado adyacente al Ðθ en el triángulo rectángulo

b₁ = medida del lado opuesto al Ðθ

c₁ = medida de la hipotenusa

La relación  =  se puede resumir de la siguiente manera. Para un ángulo agudo θ en cualquier triángulo rectángulo, la razón de la medida de su lado adyacente con la medida de la hipotenusa es la misma sin importar el tamaño del triángulo.  A esta razón se le da el nombre de coseno de θ (se abrevia cos θ).

Esta razón de la medida del lado opuesto con la medida de la hipotenusa se conoce como el seno de θ (abreviado sen θ). 

Ley del Seno

Cuando queremos resolver triángulos rectángulos recurrimos a las reglas trigonométricas tradicionales que sirven para esos propósitos. Sin embargo, cuando tratamos de resolver triángulos que no tienen ángulos rectos (oblicuos) necesitamos otras herramientas que nos permitan trabajar.

otras dos partes del triángulo. Estas pueden ser dos lados, dos ángulos o un ángulo y un lado. Resumiendo el argumento anterior de una manera mas clara necesitaríamos tener una de las siguientes combinaciones para trabajar.

·         Dos ángulos y un lado (AAL ó ALA)

·         Dos lados y un ángulo opuesto a ellos (LLA)

·         Tres lados (LLL)

·         Dos lados y el ángulo incluido (LAL)

Los primeros dos casos de nuestra lista se pueden resolver con la Ley del Seno.  Veamos en que consiste nuestra ley.  Si ABC es un triángulo con lados    entonces:

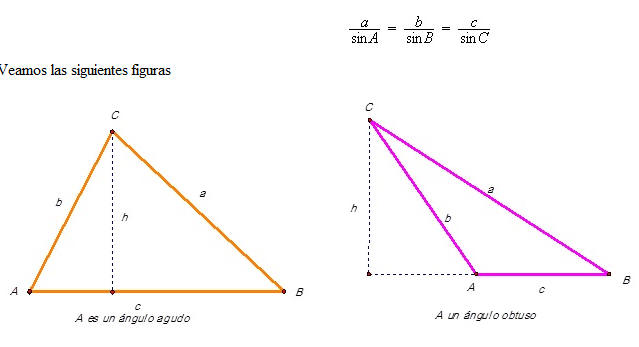
Ejemplo 1.  Caso (AAS)

Para el triángulo en la figura que sigue, se tienen las siguientes medidas:

C=102.3  , B=28.7  , b=27.4 pies. 

Halle las medidas de los restantes lados y ángulos.

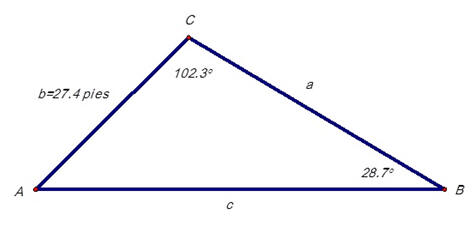
Para poder trabajar nos falta la medida del tercer ángulo. Esta estaría dada por la diferencia que hay entre 180 y la suma de las medidas que conocemos. Recuerda que las medidas de los ángulos del interior de un triángulo

Suman 180   .

Despejando por    , tendríamos pues

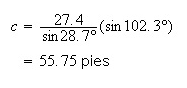
Ejemplo 2.  Caso (ALA)

 Un poste se inclina ligeramente hacia el sol formando un ángulo de 8   con la vertical. Esto provoca que proyecte una sombra de 22 pies de largo. El ángulo de elevación desde la punta de la sombra hasta el tope del poste es de 43  . Diga cuál es la altura del poste.

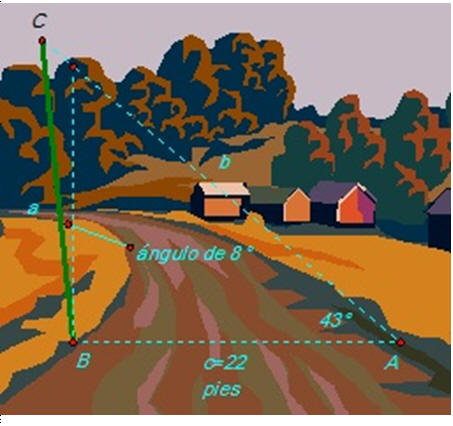
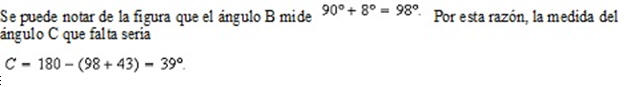
Ejemplo 3. (LLA)

Resuelva el triángulo que tiene las siguientes condiciones.

Para ello, veamos la figura representativa de nuestro caso.

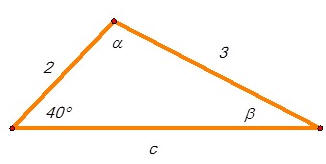
Podemos proceder a calcular la medida del ángulo    utilizando la Ley de Senos y los valores conocidos. Veamos

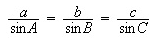
Resolviendo esta proporción multiplicando cruzado, tenemos lo siguiente

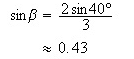
Nota: El uso de una calculadora gráfica o científica esta permitido usualmente para realizar los cómputos correspondientes en este tipo de ejercicio. De igual forma, puedes utilizar programados de aplicación que te permitan visualizar estos conceptos con más claridad.

Ley de Cosenos

La Ley de los Cosenos surge debido a la necesidad de trabajar ciertos triángulos oblicuos cuyas condiciones no se ajustan a la Ley del Seno. Estos son los triángulos que responden a las condiciones LLL y LAL.  No es difícil ver que si tenemos estas condiciones, no podemos formar las proporciones apropiadas con el uso de la Ley del Seno. Ley de los Cosenos dice:

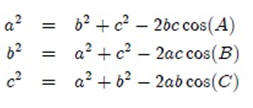
Ejemplo 1.

Resuelva el triángulo que tiene las condiciones que se indican abajo.  En este caso, los ángulos A,B,C están representados por las letras griegas  a,  b, g  respectivamente. En ambos casos su significado es el mismo en términos de que representan la medida de los ángulos correspondientes al vértice donde se  encuentren.

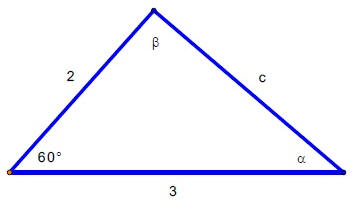
Utilizando la Ley de los Cosenos, tenemos:

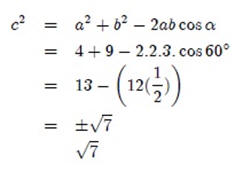
Recuerda que la raíz negativa no podemos considerarla como una alternativa en estos casos debido a que estas cantidades representan medidas con dimensiones reales. Para hallar las medidas restantes podemos usar también la Ley de los Cosenos.

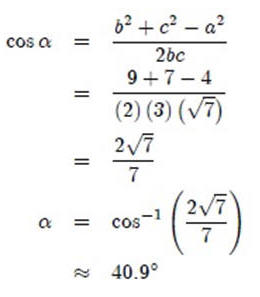
Para calcular b :

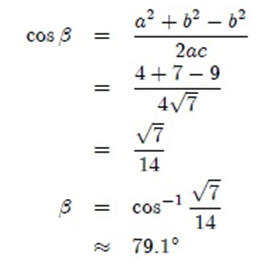
Para corroborar nuestro resultado, vamos a sumar los ángulos obtenidos. Se supone que nuestras medidas sumen 180°

Observa el siguiente ejemplo donde se trabaja con un triángulo del tipo LLL.

Ejemplo 2. Resuelva el triángulo siguiente.

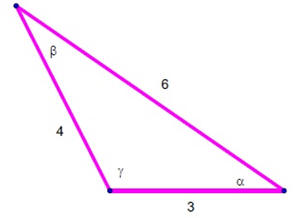
Podemos establecer las siguientes relaciones para investigar nuestros ángulos.

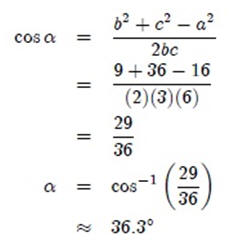
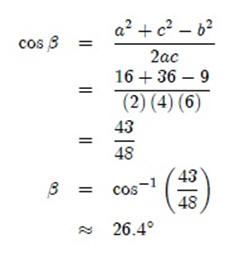
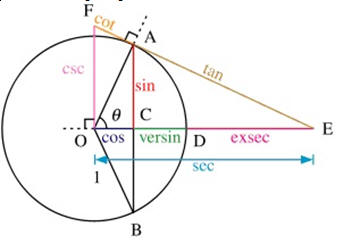
Funciones trigonométrica

En matemática, las funciones trigonométricas son funciones de un ángulo; tienen importancia en el estudio de la geometría de los triángulos y en la representación de fenómenos periódicos, entre otras muchas aplicaciones. Se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo que contiene al Ángulo, y pueden definirse igualmente como la longitud de varios segmentos partiendo de un círculo que represente a la unidad.

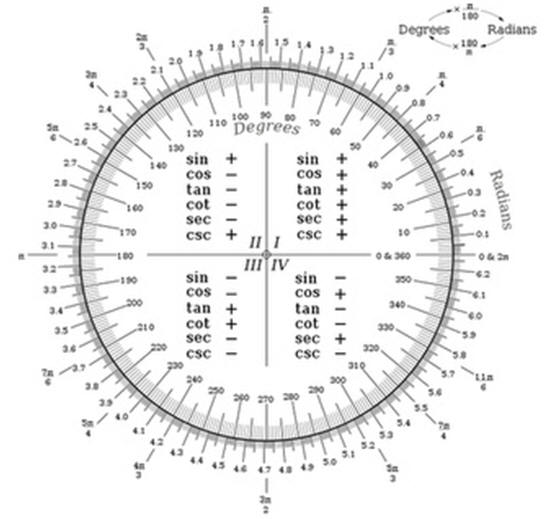
El dominio de las funciones seno y coseno es el conjunto de los números reales. para investigar su campo de valores debemos referirnos al círculo unitario.  Las funciones seno y coseno se dice que son periódicas. Esto quiere decir que si añadimos una revolución adicional a un ángulo cualquiera en el círculo unitario, regresaremos exactamente al mismo lugar donde se encontraba el lado terminal del ángulo antes de completar la revolución adicional. Los ángulos resultantes serán coterminales. Esto quiere decir que sus lados terminales coincidirán unos con otros.

Una función f es periódica, si existe un número real c tal que para toda x en el dominio de f. El valor mas pequeño de c para el cuál la función  es periódica se define como el período de la función.

Definiciones

La amplitud es por lo que es multiplicada la ecuación entera, en este caso 3

Período usted toma 2pi / (número antes de paréntesis) así que la respuesta es pi

El desplazamiento de fase es pi/2 a la izquierda si fuera negativo él sería pi/2 a la derecha

La rotación vertical es 2 unidades abajo si fuera positivo que sería 2 unidades para arriba.

Ejemplo:

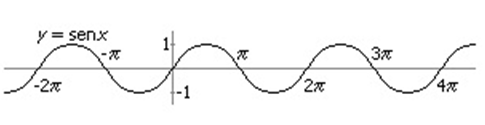
La función seno es la función definida por: f(x)= sen x.

Características

1. Dominio: IR

Recorrido: [-1, 1]

2. El período de la función seno es 2 π.

3. La función y=sen x es impar, ya que sen(-x)=-sen x, para todo x en IR.

4. La gráfica de y=sen x intercepta al eje X en los puntos cuyas abscisas son: x =n π. para

todo número entero n.

5. El valor máximo de sen x es 1, y el mínimo valor es -1.

La amplitud de la función  y=sen x es 1.

Ejemplo:

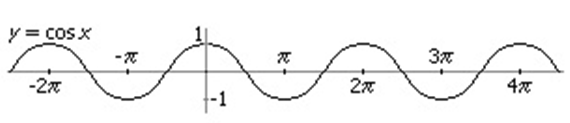
La función coseno es la función definida por: f(x)= cos x.

Características

1. Dominio: IR

Recorrido: [-1, 1]

2. Es una función periódica, y su período es 2 π.

3. La función y=cos x es par, ya que cos(-x)=cos x, para todo x en IR.

4. La gráfica de y=cos x intercepta al eje X en los puntos cuyas abscisas son:

x = π/2 + n π para todo número entero n.

5. El valor máximo de cos x es 1, y el valor mínimo valor es -1.

La amplitud de la  función y=cos x es 1.

Ejemplo:

La función tangente es la función definida por: f(x)= tan x..

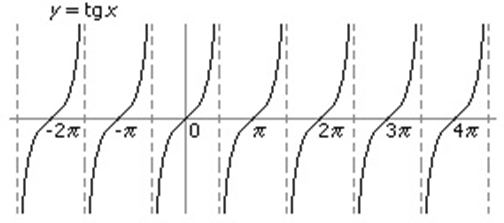
Características

1. Dominio:

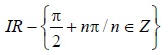
Recorrido: IR

2. La función tangente es una función periódica, y su período es π.

3. La función y=tan x es una función impar, ya que tan(-x)=-tan x.

4. La gráfica de y=tan x intercepta al eje X en los puntos cuyas abscisas son: x =n π, para todo número entero n.

Ejemplo:

Sam salta en un trampolín en una competencia internacional.   La grafica muestra la altura a la que están sus pies del suelo.

a-      Halla el periodo

b-      Halla la frecuencia

c-      Halla la amplitud

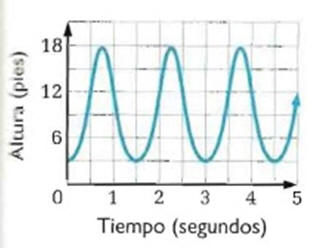
a-      periodo es 1.5 s

b-      la frecuencia es 2/3 ciclo por s

c-      la amplitud es 7.5 pies

Aplicación

Asignación 1: Valor 20 pts.

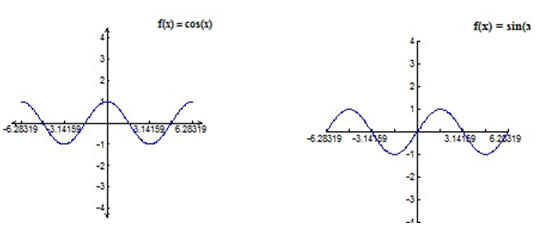
1- Identificar la función seno y la función coseno

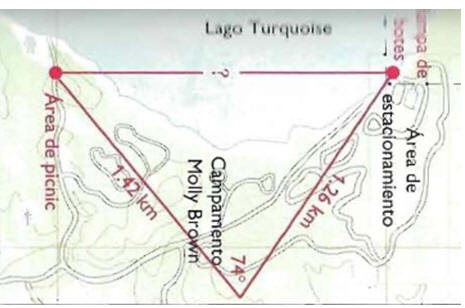
2-Halla la distancia desde el área de picnic hasta la rampa de botes al otro lado del LagoTurquoise. Utiliza la Ley del Coseno para resolver el problema.

Solución

1- Solución

2- La rampa de botes esta aproximadamente a 1.6 km del área de picnic.

© Derechos Reservados

Escuela Virtual de Educación Acelerada Proyecto Salón Hogar Inc.