|
|
Si
tenemos dos conjuntos A y B, y tratamos de armar todos los pares posibles
formados por un elemento del conjunto A y un elemento del conjunto
B, obtendremos el producto
cartesiano de los dos conjuntos.
Se escribe:  |
|
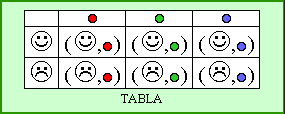
Podemos representarlo
de diferentes formas: diagramas
de flechas, diagramas
arbolados, tablas
y gráficos
cartesianos. Cada par que formemos con un elemento de
A y uno de B, en ese orden, recibe el nombre de par
ordenado. |
|
|
|
Llamaremos producto cartesiano de dos conjuntos que
simbolizaremos como AXB a todos los pares de elementos ordenados
que podamos formar tomando como primer elemento un elemento del
conjunto A y como segundo un elemento del conjunto B
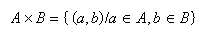
Ejemplo:
Sea los conjuntos A={1,2,3} y B={4,5,6} se tiene:
AXB={(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5) ,(3,6)}
El producto cartesiano AXB no es igual al producto cartesiano
BXA
Si los conjuntos A y B tienen elementos comunes, entonces los
elementos del producto cartesiano de la forma (a,a), se les
llama elementos diagonales.
Si el producto cartesiano fuese de un mismo conjunto AXA
puede escribirse de forma simbólica como A2.
Si el producto cartesiano lo forman más de dos conjuntos los
elementos del producto cartesiano lo formaran grupos de
elementos tomados ordenadamente de cada uno de los conjuntos que
lo forman tomando un elemento del primer conjunto, otro del
segundo otro del tercero y así hasta llegar al ultimo.
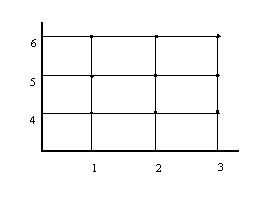
Para representar gráficamente el producto cartesiano
utilizaremos la representación cartesiana que consiste en trazar
unos ejes perpendiculares, en el eje horizontal colocaremos los
elementos del conjunto A y en el eje vertical los elementos del
conjunto B,los elementos del producto cartesiano los forman los
puntos de intercepción que se obtienen al trazar por los
elementos del conjunto A paralelas al eje vertical y por los
elementos del conjunto B paralelas al eje horizontal.
Ver la representación del ejemplo
Para saber el número de elementos del producto cartesiano nos
fijaremos en el diagrama de árbol
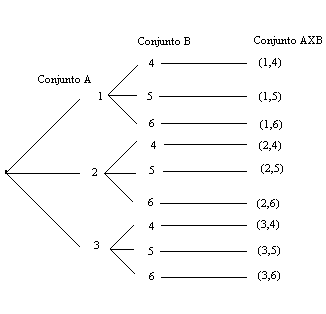
tenemos nueve
elementos, que es el resultado de multiplicar el número de
elementos del conjunto A por los del conjunto B
Podemos saber el número de elementos de un producto
cartesiano formado por n conjuntos, multiplicando el número de
elementos de cada uno de los conjuntos que intervienen
card(AXB....Z)=card(A)card(B).....Card(Z)
Correspondencias entre conjuntos
Llamamos correspondencia entre los conjuntos A y B y que
representaremos por la letra f, a cualquier subconjunto del
producto cartesiano AXB.
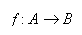
Una
correspondencia presenta los siguientes elementos
Elementos homólogos
Se dice que dos elementos a, b son homólogos en la
correspondencia f cuando el par (a, b) pertenece al subconjunto.
es decir:
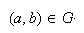
Siendo G el subconjunto.
La primera componente del par (a,b) que pertenece a G se
llama elemento original, mientras que la segunda componente
recibe el nombre de elemento imagen. Cuando b es el elemento
imagen del a por la correspondencia f escribiremos b = f(a)
Conjunto inicial.
Llamaremos así al conjunto A
Conjunto final.
Es el conjunto B
Conjunto original.
Se llama conjunto original, y lo designaremos por orig(f) al
conjunto formados por todos los elementos de A que son elementos
originales por la correspondencia f.
Conjunto imagen
Se llama conjunto imagen,y se representa por imag(f) al
conjunto formados por todos los elementos de B que son elementos
imágenes por la correspondencia f.
Grafo de la correspondencia
Se llama grafo de la correspondencia al subconjunto.
Correspondencia inversa
Se llama correspondencia inversa a la correspondencia que
resulta de cambiar el orden de los conjuntos AXB por BXA
La correspondencia inversa la designaremos por f-1
Ejemplo:
Sea f la correspondencia definida por el grafo:
G={(a,1),(a,2),(b,3),(c,5)}
La correspondencia inversa f-1 será:
G-1={(1,a),(2,a),(3,b),(5,c)}
Aplicaciones
Se llama aplicación entre los conjuntos A y B a la
correspondencia de A en B tal que:
Todos los elementos de A son elementos originales El
transformado de cada elemento es único
Aplicación suprayectiva
Se llama así una aplicación donde el conjunto final coincide
con el conjunto imagen: esto es, cuando todos los elementos de B
son elementos imágenes de algú elemento de A.
f suprayectiva equivale a Card(A) es mayor o igual a Card(B)
Aplicación inyectiva
Se llama así a una aplicación de A en B donde cada elemento
imagen lo es de un solo original.
f inyectiva equivale a Card(A) es menor o igual a card(B)
Aplicación biyectiva
Se llama así a una aplicación de A en B donde es al
supreyectiva e inyectiva.
Para que una aplicación sea biyectiva es necesario que ambos
conjuntos tengan el mismo número de elementos.
Aplicació inversa
Si la aplicación es biyectiva la correspondencia inversa
siempre será una aplicación
Aplicació Compuesta
Si tenemos una aplicación f de A en B y otra aplicación g de
B en C, tal que imag(f) =o rig(g); llamaremos aplicación
compuesta y denotaremos por 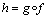 a
una nueva aplicación de A en C definida del siguiente modo: a
una nueva aplicación de A en C definida del siguiente modo:
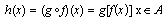
Relaciones binarias
Se llama relación binaria definida en un conjunto A a la
correspondencia de A en A
Propiedades que pueden cumplir las relaciones binarias son:
Reflexiva, simétrica, antisimétrica y transitiva
Reflexiva
Se llama relación reflexiva cuando un elemento esta
relacionado con sigo mismo y se escribe aRa para todo a que
pertenece al conjunto.
Simétrica
Se llama relación simétrica si para todo par de elemento
ocurre que el elemento a esta relacionado con el elemento b,
entonces el elemento b esta relacionado con el elemento a.
Antisimétrica
Se llama relación antisimétrica si para todo par de elemento
ocurre que el elemento a esta relacionado con el elemento b,
entonces el elemento b esta relacionado con el elemento a, y
además, se deduce que a = b.
Transitiva
Se llama así cuando se verifica que si el elemento a esta
relacionado con el elemento b y el elemento b esta relacionado
con el elemento c; entonces el elemento a esta relacionado con
el elemento c.
Leyes de composición
Se dice que en A se ha definido una ley de composición
interna u operació cuando se define una aplicación del producto
cartesiano AXA en A de tal forma que el par de elementos (a,b)
genere otro elemento c, tal que c también pertenece al conjunto
A.
Para representar el elemento imagen del par (a,b) se utiliza
la notación c=afb donde f es cualquier simbolo. Por ejemplo
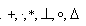
Se dice que en A se a definido una ley de composición externa
sobre el conjunto B cuando se define una aplicación del producto
cartesiano BXA en A
A los elementos del conjunto B se les llama escalares.
llamando a a los elementos pertenecientes al conjunto A y b a
los elementos que pertenecen al conjunto B tenemos que c=afb,
donde c pertenece al conjunto A
Propiedades de las leyes de composición
Asociativa
Se dice que la ley de composición * es asociativa cuando para
cualquier elementos a,b,c pertenecientes al conjunto A se
verifica:
(a * b) * c = a * (b * c)
Conmutativa
Se dice que la ley de composición * es conmutativa cuando
para cualquier elementos a,b,c pertenecientes al conjunto A se
verifica:
a * b = a * b
Elemento neutro
Se dice que la ley de composición * posee elemento neutro
cuando existe un elemento n de A tal que cualquiera que sea a
perteneciente al conjunto A se verifica:
a * n = a
Elemento simétrico
Se dice que la ley de composición, que posee elemento neutro,
es simetrizable cuando para cualquier elemento de a
perteneciente al conjunto A existe un elemento a' de A tal que:
a*a'=n
Donde n es el elemento neutro
Distributiva entre dos operaciones
Se dice que la ley de conposición * es distributiva respecto
de la operación ¤ cuando cualquiera que sean los elementos a, b,
c pertenecientes al conjunto A se verifica:
a * (b ¤ c)= a * b ¤ a * c
Estructuras algebraicas
Se llama estructura algebraica a todo conjunto en la que se
han definido una o varias leyes de composición
Estructuras algebraicas con una ley de composición
Semigrupo
Se dice que el conjunto A con la ley de composición interna *
tiene estructura de semigrupo si la ley es asociativa.
Si la operación * posee la propiedad conmutativa o elemento
neutro o ambas a la vez, el semigrupo se llama conmutativo, con
elemento neutro o conmutativo con elemento neutro,
respectivamente.
Grupo
Se dice que el conjunto A con la ley de composición interna *
tiene estructura de grupo si la ley es asociativa, posee
elemento neutro y es simetrizable.
Si la operación * posee la propiedad conmutativa, entonces el
grupo se llama conmutativo o abeliano.
Estructuras algebraicas con dos leyes de composición
Semianillo
Se llama semianillo cuando en el conjunto A hemos definido
dos leyes de composición interna que tienen estructura de
semigrupo y además una ley de composición es distributiva
respecto a la otra.
Anillo
Se llama anillo cuando en el conjunto A hemos definido dos
leyes de composición interna una que tiene estructura de grupo y
la otra de semigrupo y además una ley de composición es
distributiva respecto a la otra.
Cuerpo
Se llama cuerpo cuando en el conjunto A hemos definido dos
leyes de composición interna que tienen estructura de grupo y
además una ley de composición es distributiva respecto a la otra.
Espacio vectorial
Se llama espacio vectorial a la estructura en la que se ha
definido sobre el conjunto A una estructura de cuerpo
conmutativo i una ley externa sobre el conjunto B que satisfacen
las siguientes condiciones:
A con la ley * es un grupo conmutativo
Distributiva de la ley externa ¤ respecto de la interna * en
A
Distributiva de la ley externa ¤ respecto de la enterna * en
B
Asociativa mixta
Neutralidad de la ley externa
|